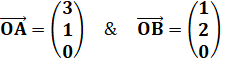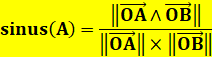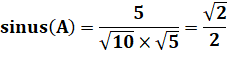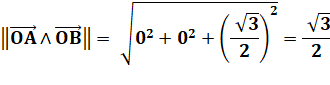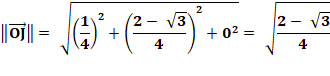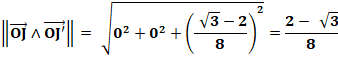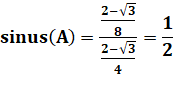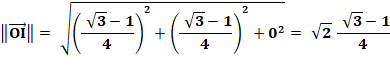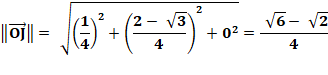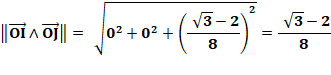Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 01/07/2023 M'écrire Brèves de Maths

INDEX Géométrie Angles Trigonométrie	Géométrie Analytique
	Droite	Cercle	Rectangle	Aire du triangle
	Quadrilatère	Parallélogramme	Parallélépipède	Calcul du sinus

Faites un double-clic pour un retour en haut de page

Calcul du SINUS d'un angle avec le produit vectoriel Comment calculer l'angle entre deux droites connaissant les coordonnées de points sur ces droites. Le produit vectoriel est fait, notamment, pour cela. Voyons comment pratiquement utiliser cette formule.
	Sommaire de cette page >>> Calcul du sinus de l'angle >>> Angle du triangle équilatéral >>> Triangles équilatéraux dans le carré >>> Dodécagone dans le carré	Débutants Géométrie Glossaire Géométrie

Calcul du sinus de l'angle		haut
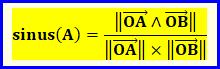
Comment calculer la valeur d'un angle en connaissant les coordonnées du sommet et celles de deux points de côté ? Chaque côté de l'angle est associé à un vecteur. Le sinus de l'angle est alors le rapport entre la norme du produit vectoriel et le produit des normes des vecteurs.
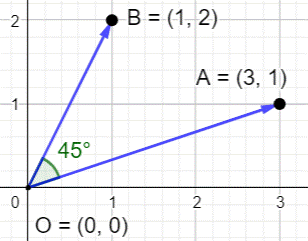
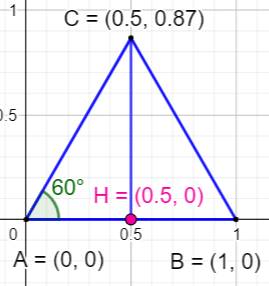
Angle et vecteurs L'angle est définit par son origine O et deux points A et B situés chacun sur un des côtés. Les segments OA et OB sont alors considérés comme des vecteurs. Leur produit vectoriel définit le sinus de l'angle entre ces vecteurs. Comment ? Introduisons quelques notions.
Notation des vecteurs Entre parenthèses, on note les trois coordonnées en x, y et z. Notons que dans le plan, les coordonnées en z sont nulles.
Produit vectoriel Donnons la méthode du calcul du produit vectoriel. Pour un calcul pratique, faire la copie (en rose) des deux premières lignes. Puis, calcul des trois différences des produits en croix. Les nombres obtenus sont les coordonnées d'un nouveau vecteur. En l'occurrence x et y sont nuls. Ce vecteur est donc perpendiculaire au plan contenant OA et OB.
Normes des vecteurs La norme spécifie la longueur du vecteur. C'est la racine de la somme des carrés des coordonnées.
Angle entre vecteurs Le sinus de l'angle est égal à cette fraction entre les normes. Ici, le calcul numérique de l'angle correspond bien à la valeur indiquée sur la figure.

Voir Brève 51 - 1015

Angle du triangle équilatéral		haut
On se propose de retrouver la valeur des angles du triangle équilatéral avec la méthode du produit vectoriel.
Vecteurs On sait que la hauteur du triangle équilatéral mesure √3/2. Coordonnées des points, extrémités des vecteurs
Produit vectoriel
Normes	Calcul de l'angle

Triangles équilatéraux dans le carré (1/2		haut
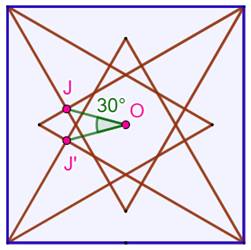
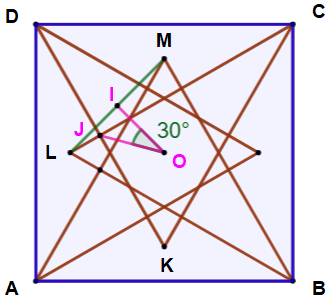
Construction Un carré bleu et quatre triangles équilatéraux accolés intérieurement au carré. Deux points d'intersections J et J'. Montrer que l'angle JOJ' vaut 30°. Géométrie (figure du bas) Angles des triangles équilatéraux: 60° (bleu). Angles élémentaires en C, par différence: 30° (bleu). CL est un des bissectrices du triangle équilatéral, c'est aussi la médiatrice et, le point J est le milieu de DK. 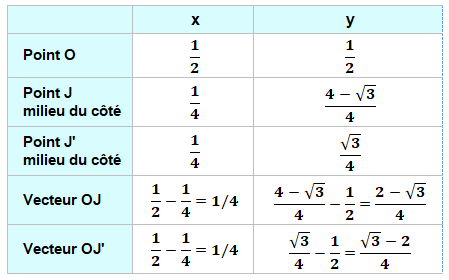De même le point J' est le milieu de AM. Il est alors possible de calculer les coordonnées des points J et J'. On retient que la hauteur d'un triangle équilatéral vaut √3/2. Coordonnées des points J et J' Système d'axes orthonormé: AB, AD avec AB = AD = 1.
Produit vectoriel
Normes	Calcul de l'angle

Triangles équilatéraux dans le carré (2/2		haut
Construction On trace le point I milieu de LM. Montrer que l'angle IOJ vaut 30°. Coordonnées des points I et J
Produit vectoriel
Normes	Calcul de l'angle

Dodécagone dans le carré		haut
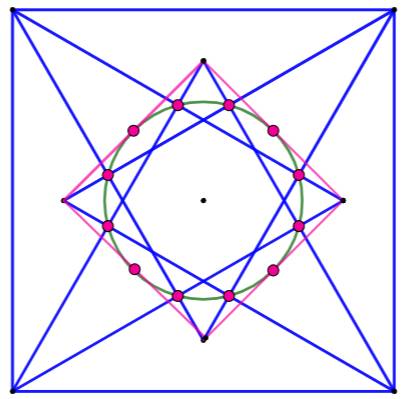
Construction Un grand carré avec ses quatre triangles équilatéraux inscrits sur les côtés. Le carré rose reliant les sommets libres des triangles équilatéraux. Les milieux des côtés. Le cercle qui passe par ces milieux passe aussi par les points d'intersection entre triangles. Soit 12 points cocycliques. Ce sont les sommets d'un dodécagone régulier. Le démontrer ! Ce qu'il faut savoir La hauteur du triangle équilatéral vaut: √3/2. Les coordonnées du point milieu est la demi-somme des coordonnées des extrémités. La longueur d'un segment se calcule avec e théorème de Pythagore.
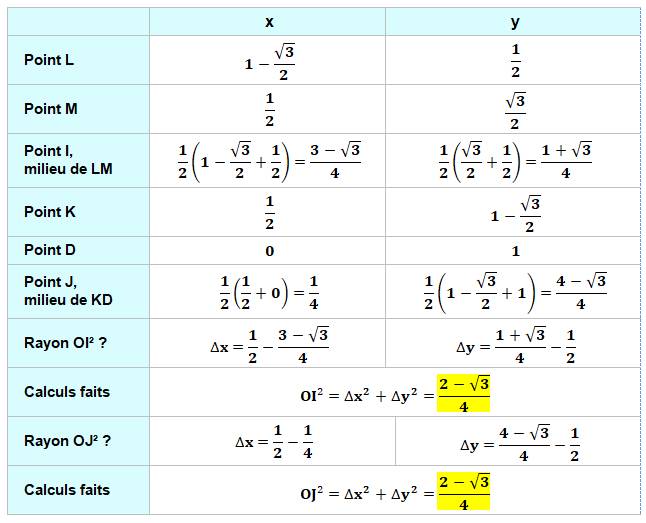
Démonstration Les deux paragraphes précédents montrent que tous les point de type I, J et J' forment des angles de 30 degrés. Les points sont situés sur 12 rayons régulièrement espacés.	Il faut aussi montrer que les points sont à égales distance du centre. Le montrer pour deux d'entre eux (OI et OJ) sera suffisant.
Calculs montrant que OI = OJ (même notation que plus haut)

Voir Brève 51 - 1016

Haut de page (ou double-clic)

Suite	Aire du quadrilatère – Méthode analytique Aire du triangle – Méthode analytique Calcul analytique d'une intersection
Voir	Géométrie – Index Ovales de Cassini Fonction affine
Cette page	http://villemin.gerard.free.fr/aMaths/GeomAnal/SinusPV.htm