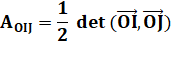|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Aire du TRIANGLE Calcul à partir des
coordonnées des sommets À partir d'un
exercice, examen de trois méthodes analytiques de calcul de l'aire
d'un triangle quelconque. |
Anglais: how to find the area
of a triangle given three vertices?
Area of a triangle by
formula – Coordinate geometry
Voir Aire
du triangle – Toutes les formules
|
|
||
|
Données Carré
ABCD et son centre O; Point I
symétrique de A par rapport à B; Point J
symétrique de D par rapport à A; et Triangle
OIJ. Questions En
utilisant le repère
orthonormé (A; B, D):
|
|
|
|
|
||
|
Repère orthonormé (A;
B,D)
Coordonnées des points Indication sur la figure des coordonnées
des points utiles. Le point H Le point H, milieu du segment IJ, a
été introduit. Quelle est sa propriété ? Le triangle étant isocèle (on va le démontrer), le
segment OH est une des hauteurs du
triangle isocèle (et aussi, médiane, médiatrice et bissectrice de
l'angle en O) >>> |
|
|
|
|
||
|
Observation On note
tout de suite que => Mais il faut
montrer cette égalité avec un calcul utilisant les
coordonnées. |
Pour le segment OI: longueur en x = 1,5 et longueur en y = 0,5. Pour le segment OJ: longueur en x = 0,5 et longueur en y = 1,5. Ce sont les mêmes valeurs
(symétriques) => OI = OJ. Le triangle OIJ est bien isocèle. |
|
|
Longueur
de OI |
= (2 –
1/2)² + (0 – 1/2)² = (3/2)²
+ (–1/2)² = 5/2 |
|
|
Longueur
de OJ |
=
(0 – 1/2)² + (–1 – 1/2)² = (–1/2)² + (–3/2)² = 5/2 |
|
|
Conclusion |
Deux des côtés du triangle OIJ sont égaux, il est isocèle en O. |
|
|
|
||
|
Base IJ
du triangle OIJ |
IJ² = 1² + 2² = 5 En lisant les longueurs sur la figure |
|
|
Hauteur
OH (H milieu de IJ) |
OH² = 1² + (1/2)² = 5/4 |
|
|
A = ½ IJ x OH = ½ √5 x √5/2 = 5/4 = 1,25 |
||
|
Je me
rassure avec le logiciel GeoGebra Confirmation
que l'aire vaut un quart de plus que l'aire du carré unité.
En
passant, on vérifie que OJ
et IO mesurent: 1,58 comme nous l'avions trouvé plus haut. On note
également les coordonnées du point H (1, –1/2). |
|
|
|
|
||
|
La méthode 1 utilise cette méthode classique: aire =
½ côté x hauteur |
||
|
Aire du
triangle OIJ |
A = ½ IJ x OH On a vu que OH est la hauteur du triangle
isocèle issue de O. |
|
|
Longueur
de IJ (carré) |
= (0 –
2)² + (–1 – 0)² = 2² + 1² = 5 |
|
|
Coordonnées
du point H |
XH = ½ (XI
– XJ) = ½ (2 – 0) = 1 YH = ½ (YI
– YJ) = ½ (0 – 1) = –1/2 |
|
|
Longueur
de OH (carré) |
= (1 –
1/2)² + (–1/2 – 1/2)² = (1/2)²
+ (-1)² = 1/4 + 1 = 5/4 |
|
|
Aire |
|
|
|
|
||
|
Cette méthode est du
niveau lycée (seconde).
|
||
|
Formule
de l'aire d'un triangle connaissant les coordonnées des sommets |
|
|
|
Avec les valeurs
numériques |
A = ½ {1/2 (0 – (–1)) + 2 ((–1) – 1/2)
+ 0 (1/2 – 0)} =
½ { 1/2 – 3 + 0 } =
–1/2 x 5/2 =
–5/4 A = 5/4 (la valeur positive) |
|
|
|
||
|
Cette méthode est
d'un niveau supérieur. Elle suppose la connaissance des matrices. Elle connue pour donner
l'aire du parallélogramme
engendré par les deux vecteurs. |
||
|
Formule de l'aire
d'un triangle connaissant deux vecteurs comme côtés. |
|
|
|
Avec les
valeurs numériques |
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()