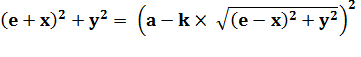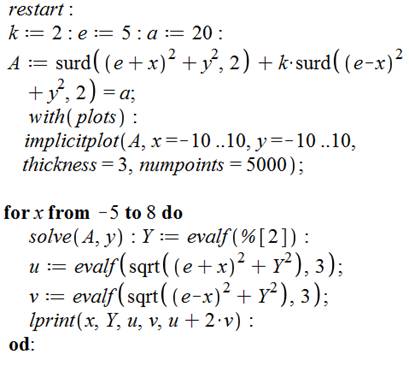|
|||||||||||||||||||||||||||||||||||||||
![]()
|
COURBES OVALES particulières Cassini et Descartes Ellipses
et ovales, particularités, équation et allure du graphe Avec
calcul complet de l'équation et programmation pour l'ovale cartésien. |
|
|
||
|
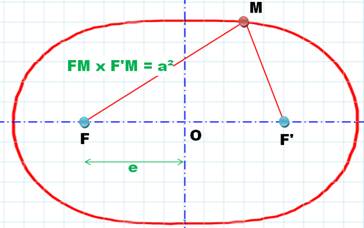
Ovale de
Cassini: lieu des points tels que le produit FM.FM' est constant. Avec FM.FM' = a² et FF'
= 2e, l'équation
s'écrit: (x² + y²)² – 2e² (x² – y²) – a4 + e4
= 0 Illustration (en bas) avec e = 6 et Rouge: a =
8,5 (externe) Bleue: a = 8 Rouge: a = 6 Bleue: a = 4 Allure selon a comparé à e
|
|
|
|
|
||
|
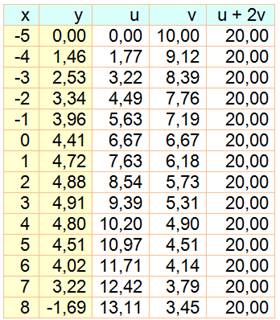
Ovale de Descartes ou
cartésien: lieu des points tels que la somme FM +k.FM' est constante. Le nombre
k est rationnel. Avec FM + k.FM' = u k.v = a et FF'
= 2e, Équation
Illustration k = 2 e = 5 a = 20 Équation
Quelques valeurs
(et leurs opposées en y)
|
|
|
|
Calcul de l'équation sans radicaux |
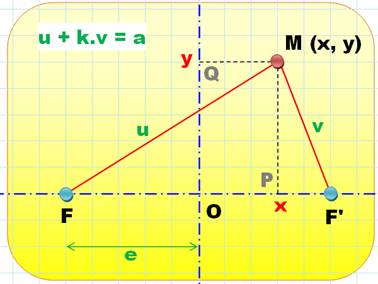
Les coordonnées du point M
sont: x et y qui doivent être exprimées en fonction de a et e. |
|
Théorème
de Pythagore dans les triangles rectangles FMP
et F'MP. |
u² = (e + x)² + y² v² = (e – x)² + y² |
|
À noter |
u² – v² = 4ex u² + v² = 2(x² + y² + e²) Rien à tirer de
plus; il faut malheureusement passer par u + kv =
a, avec des racines carrés. Il faudra élever
au carré pour éliminer les radicaux, avec les artefacts (solutions en plus)
inhérentes à cette opération. |
|
Notre relation à maintenir ente u et v: |
u + k.v = a
|
|
Au carré |
|
|
En isolant le radical à droite |
|
|
À nouveau au carré |
|
|
Programmation avec Maple de la formule
SANS RADICAUX (avec élévations au carré) (explications
supposant un minimum de connaissance de Maple) Pour calcul des valeurs et surtout exécuter le
graphe. Ce programme comporte quelques précautions pas
évidentes a priori. |
|
|
|
Programme – Commentaire A est le premier membre de la formule; B est le second; chacun avant
leur mise au carré. Justement B comporte le radical sous la forme surd
et non root Chaque expression est développée (expand) et
ordonnée en x et en y (collect). Simple
vérification des formules (voir affichage). Passage à une application numérique avec affichage des formules A et
B. Tracé du graphe en x et y (implicitplot)
avec le package (plots). La fonction tracée ici est A² = B²pour respecter la formule trouvée
sans radical. On aurait tout aussi bien pu prendre A = B. Spécification d'une précision à 5 000 points (200 par défaut). Calcul de y,
u et v à partir d'un valeur de x à préciser ici. Résolution de l'équation en y et affichage des 2 à 4 racines
possibles. Choix de la racine (ici, la 2e) et calcul de u et v.
Affichage de toutes ces valeurs. Le choix de la racine se portera sur celle qui donne u + 2v = a = 20,
les autres étant des artefacts (résultats imaginaires) dus aux élévations au
carré. |
|
|
Formule A. Son développement ordonné. Formule B. Le développement ordonné de B². Formule A avec instanciation numérique. Idem pour B. |
|
|
Tracé du graphe Deux parties: Au centre, le petit ovale, le graphe vu plus haut. En périphèrie, une solution également valable, créée du fait de la mise
au carré. Elle résulte de valeurs imaginaires en Y. Par contre, les valeurs
de u et v sont bien réelles. Les deux foyers sont bien en y = 0 et x = -5 et 5. La somme u + 2v est
égale à 20 pour tous les points des courbes en rouge. |
|
|
Affichage des valeurs pour x = 0 Deux ordonnées y en -4,43 et 4,
43 (courbe centrale et y = -19,4 et 19,4 pour la courbe externe. Exemple de calcul avec x = 0 et y = 4,409… de u et v chacun valant 6,
66… et, le triple valant bien a =
20. |
|
Programmation avec Maple de la formule primitive
AVEC RADICAUX Voir les explications >>> |
|
|
|
Programme – Commentaire Introduction des valeurs numériques. La formule directe avec les radicaux (surd). Affichage de la formule instanciée avec les valeurs numériques. Package plots et tracé avec implicitplot. Avec x de -5 à + 8, calcul numérique de y; u et v; puis, impression de
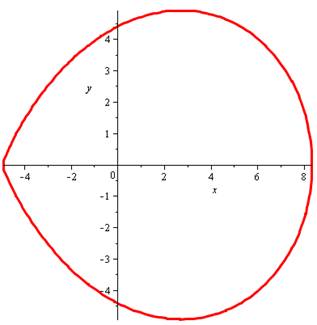
ces valeurs Formule instanciée Ovale de Descartes PUR: la courbe centrale du graphe précédent, sans
la courbe externe obtenue en passant par des valeurs intermédiaires complexes. Affichage des valeurs numériques. Dan l'ordre sur chaque ligne x, puis un des valeurs de y (la seconde donnée par solve) Suivis des valeurs de u et v avec précision de trois chiffres
seulement. Enfin la valeur de u + 2v qui doit valoir a = 20. |
Bilan
|
Grande prudence avec les formulations avec
radicaux Avec un outil mathématique, se contenter de la solution
directe même avec des radicaux.
>>> La solution éliminant les radicaux nécessite au moins une
élévation au carré qui introduit des artéfacts. Certains prolongent la
solution via les nombres complexes; d'autres sont à rejeter. >>>
Prudence informatique Pour le calcul de la racine carrée: emploi de l'instruction surd et non sqrt ou encore de la
puissance ½ >>> Pour le tracé, l'instruction plot
trace y = f(x), alors qu'implicitplot
permet le tracé de fonction en x et en y. Pour obtenir de belles courbes, précisez la quantité de
points à calculer avec numpoints. La résolution d'équations
avec solve
produit toutes les solutions, réelles ou complexes. |
Voir Racines / Racines carrées / Programmation
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Geometri/Coniques/Cassini.htm
|
![]()