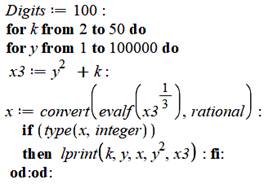Equation de Bachet, équation de Mordell

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/05/2019 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Théorie des NOMBRES
Débutants Général	Courbes elliptiques			Glossaire Ellipse / Elliptique
INDEX Théorie des nombres	Introduction	Nombres congruents	Vers l'elliptique
	Eq. de Bachet	Rang des courbes elliptiques
		Sommaire de cette page >>> Historique >>> Approche >>> Quelques solutions >>> BACHET – Solutions k < 0 >>> MORDELL – Solutions pour k > 0 >>> Bilan

Équation de Bachet-Mordell

y² = x³ + k y² – x³ = k

Différence entre carré et cube = entier.

But: déterminer les points de coordonnées entières sur ces courbes elliptiques particulières.

Équation diophantienne qui est toujours (2019) l'objet de recherches.

Habituellement: Mordell => k > 0 et Bachet => k < 0.

Claude Gaspard Bachet de Méziriac (1581-1638)

Historique
Bachet 1621	Il donne la solution du cas y² = x³ – 2. Il a su donner d'autres solutions rationnelles à partir de la solution connue en 3 et 5 (formule de duplication). Il y a donc une infinité de solutions rationnelles.
Fermat (vers1605-1665)	Prétend connaitre la méthode pour résoudre ces équations et lance à ses contemporains le défi de la trouver. Notamment démontrer qu'il n'y qu'une seule solution à y² = x³ – 2.
Lebesgue 1869	Prouve que k = 7 n'a pas de solution.
Euler 1730	Donne une réponse, mais incorrecte.
Axel Thue 1908	Il montre que ce type d'équations avec k non nul possède un nombre fini de solutions (y compris zéro).
Mordell 1922	Louis Mordell (1888-1972) démontre (1922), après Thue, qu'il n'y a, sur ces courbes, qu'un nombre fini de points à coordonnées entières lorsqu'ils existent.
1998	On connait toutes les solutions pour k jusqu'à 10 000 en positif et en négatif.

Approche
Quantité finie de solutions Le graphe de ces fonctions est une courbe elliptique. L'enjeu avec l'équation diophantienne de Bachet-Mordell est de trouver des points sur cette courbe ayant des cordonnées en nombres entiers. On a montré que ces points, s'il existe, sont en nombre limité.	Graphe général de y² = x³ + k Source image: Rational points on Elliptic Curves
Anglais

Quelques solutions
k = 1 => y² = x³ + 1 Une des plus simples à étudier. Le graphe montre toutes les solutions en positif et en négatif. Solutions: (-1,0), (0,1), (0,-1), (2,3) et (2,-3).
k = –2 => y² = x³ – 2 Ce cas fut étudié par Bachet de Méziriac en 1621. Il trouva la méthode pour produire autant de solutions rationnelles que l'on veut à partir d'une solution en nombres entiers (formule de duplication). Elle est basée sur le tracé de la tangente à la courbe au point de coordonnées entières. La troisième intersection est une nouvelle solution rationnelle. Le procédé est itératif. Il y a donc une infinité de solutions rationnelles.	Seule solution entière (double) 3³ – 5² = 27 – 25 = 2 3³ – (–5)² = 27 – 25 = 2 Solutions rationnelles (formule de duplication) Première solution rationnelle Deuxième solution rationnelle Formule générale de duplication avec c
k = –3	Aucune solution
k = +3	Pour k positif, seule solution: 2² – 1² = 4 – 1 = 3
k = –4 Fermat (1605-1665) connaissait ces deux solutions(1657). Il indique que ce sont les seules solutions. Avait-il une démonstration ?	Deux solutions 2³ – 2² = 8 – 4 = 4 5³ – 11² = 125 – 121 = 4
k = –7	2³ – 1² = 8 – 1 = 7 32³ – 181² = 32 768 – 32 761 = 7
k = –11	3³ – 4² = 27 – 16 = 11 15³ – 58² = 3 375 – 3 364 = 11

BACHET – Solutions k < 0
Programme Maple Commentaires Calculer la racine cubique nécessité de passer à un calcul avec de nombreux chiffres (ici Digits = 100). Calcul de y² + k et recherche si c'est un cube. La racine cubique (puissance 1/3) est convertie en nombre rationnel tel que, si la racine est un nombre entier, elle est détectée par son type integer (entier). Si c'est le cas, impression des valeurs de y, x et de leur puissance respectives. Liste des k sans solution 3, 5, 6, 9, 10, 12, 14, 16, 17, 21, 22, 24, 29, 30, 31, 32, 33, 34, 36, 37, 38, 41, 42, 43, 46, 50, 51, 52, 57, 58, 59, 62, 65, 66, 68, 69, 70, 73, 75, 77, 78, 80, 82, 84, 85, 86, 88, 90, 91, 92, 93, 94, 96, 97, 98, 99, … Note: les k cubes (8, 27 …) donnent des solutions triviales non listées.	k	y	x	y²	x³
	2	5	3	25	27
	4	2	2	4	8
	4	11	5	121	125
	7	1	2	1	8
	7	181	32	32761	32768
	11	4	3	16	27
	11	58	15	3364	3375
	13	70	17	4900	4913
	15	7	4	49	64
	18	3	3	9	27
	19	18	7	324	343
	20	14	6	196	216
	23	2	3	4	27
	25	10	5	100	125
	26	1	3	1	27
	26	207	35	42849	42875
	28	6	4	36	64
	28	22	8	484	512
	28	225	37	50625	50653
	35	36	11	1296	1331
	39	5	4	25	64
	39	31	10	961	1000
	39	103	22	10609	10648
	40	52	14	2704	2744
	44	9	5	81	125
	45	96	21	9216	9261
	47	13	6	169	216
	47	41	12	1681	1728
	47	500	63	25000	250047
	48	4	4	16	64
	48	148	28	21904	21952
	49	524	65	274576	274625

MORDELL – Solutions pour k > 0
Louis Mordell (1888-1972), mathématicien américano-britannique, est un spécialiste des équations diophantiennes. Exemples 3² – 2³ = 9 – 8 = 1 312² – 46³ = 97344 – 97336 = 8 Conjecture de Catalan Les nombres 8 et 9 sont seules puissances parfaites consécutives. Catalan. Voir Nombre 8 dans DicoNombre Liste des k sans solution 6, 7, 11, 13, 14, 20, 21, 23, 29, 32, 34, 39, 42, 45, 46, 47, 51, 53, 58, 59, 60, 61, 62, 66, 67, 69, 70, 74, 75, 77, 78, 83, 84, 85, 86, 87, 88, 90, 93, 95, 96, 102, … Note: les k cubes donnent des solutions triviales non listées.	k	y	x	y²	x³
	1	1	0	1	0
	1	3	2	9	8
	3	2	1	4	1
	4	2	0	4	0
	8	3	1	9	1
	8	4	2	16	8
	8	312	46	97344	97336
	9	3	0	9	0
	9	6	3	36	27
	9	15	6	225	216
	9	253	40	64009	64000
	12	47	13	2209	2197
	15	4	1	16	1
	15	1138	109	1295044	1295029
	16	4	0	16	0
	17	5	2	25	8
	17	9	4	81	64
	17	23	8	529	512
	17	282	43	79524	79507
	17	375	52	140625	140608
	18	19	7	361	343
	19	12	5	144	125
	22	7	3	49	27
	24	5	1	25	1
	24	32	10	1024	1000
	25	5	0	25	0
	28	6	2	36	8
	30	83	19	6889	6859
	35	6	1	36	1
	36	6	0	36	0
	36	10	4	100	64
	36	42	12	1764	1728
	37	8	3	64	27
	37	3788	243	14348944	14348907
	38	37	11	1369	1331
	40	16	6	256	216
	41	7	2	49	8
	44	13	5	169	125
	48	7	1	49	1
	49	7	0	49	0

Bilan

Selon les valeurs de k:

la quantité de solutions est finie (y compris 0).

on sait démontrer qu'il n'y a aucune solution pour certaines valeurs de k

on connait toutes les solutions existantes pour k jusqu'à 10 000, positif comme négatif.

Les démonstrations dans ce domaine des équations diophantiennes font appel aux outils avancés de la théorie des nombres: les nombres complexes et les fonctions elliptiques, les structures algébriques (anneau), la réciprocité quadratique, etc.

Suite	Vers l'elliptique Rang des courbes elliptiques Différences de puissances – Tables
Voir	Équations diophantiennes Conjectures – Index Actualités 2016 Théorie des nombres – Index
DicoNombre	Accès aux nombres cités: voir dans le DicoNombre
Sites	Mordell Louis Joël – ChronoMath – Serge Mehl Mordell curve – Wikipedia Examples of Mordell's Equation – Keith Conrad Mordell Curve – Wolfram MathWorld OEIS A081121 – Numbers n such that Mordell's equation y^2 = x^3 - n has no integral solutions OEIS A054504 – Numbers n such that Mordell's equation y^2 = x^3 + n has no integral solutions
Sites avancés	Autour de l'équation de Bachet – Daniel Perrin On Bachet's Equation – Clay McGowen Mordell's Equation – Keith Conrad - 2008 Mordell's Equation: An Introduction – Brian Sittinger
Cette page	http://villemin.gerard.free.fr/aMaths/ThNb/Bachet.htm