|
Édition du: 31/05/2025 |
|
INDEX
|
TOPOLOGIE |
||
|
Outils de la topologie |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Hypothèse du cobordisme Deux objets se
retrouvent progressivement réunis en un seul. L'hypothèse du
cobordisme énonce que le complexe peut être déduit d'une analyse à une
échelle plus petite. |
||
|
|
Sommaire de cette page >>> Approche >>> Cobordisme >>> Hypothèse du cobordisme >>> Résumé |
Débutants Glossaire |
|
Îles Imaginez deux îles flottant sur l'eau : si vous
pouvez construire un pont entre elles sans interruption, alors elles sont en
cobordisme. |
|
|
|
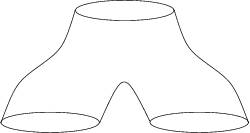
Pantalon Une image classique pour illustrer le cobordisme
est celle du pantalon topologique : imaginez un pantalon dont la taille représente
une surface et dont les deux jambes représentent une autre surface. Le pantalon lui-même est un cobordisme entre la
surface-taille et les surfaces-jambes. |
|
|
|
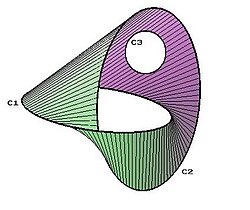
Disque à deux trous Imaginez un disque auquel on retire deux petits
cercles à l'intérieur. Ce disque est un cobordisme entre les deux
cercles internes et le cercle extérieur. Illustration avec le trou de ver (whormhole) |
|
|
|
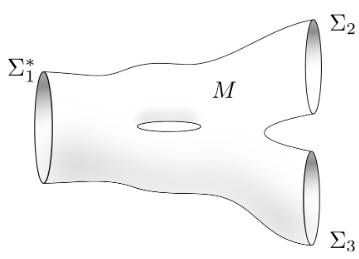
Définition Le cobordisme est une notion de topologie qui
permet de relier deux variétés compactes en les considérant comme le bord d'une
variété de dimension supérieure. En topologie différentielle, le cobordisme est
une relation d'équivalence entre variétés différentielles compactes. Deux variétés compactes M et N sont dites
cobordantes ou en cobordisme si leur réunion disjointe peut être réalisée
comme le bord d'une variété à bord compacte L. On dit alors que cette variété
L est un cobordisme entre M et N, ou bien que L réalise un cobordisme entre M
et N. L'existence d'un tel cobordisme implique que M et
N soient de même dimension. Liens entre cobordisme et topologie 1.
Classification des variétés : Le
cobordisme est utilisé pour classer les variétés en fonction de leur bord.
Deux variétés sont dites cobordantes si elles peuvent être reliées par une
variété de dimension supérieure. 2.
Groupes de cobordisme :
L'existence d'un cobordisme entre deux variétés définit une relation
d'équivalence, permettant de construire des groupes de cobordisme qui jouent un
rôle clé en topologie algébrique. 3.
Théorie des champs topologiques : Le
cobordisme est utilisé dans la théorie
quantique des champs topologiques, où les variétés et leurs
cobordismes sont interprétés comme des objets mathématiques décrivant des
transitions physiques. 4.
Applications en géométrie : Le
cobordisme est lié à la géométrie
différentielle, notamment dans l'étude des structures de
variétés et des invariants topologiques. |
Un cobordisme simple Un cobordisme plus élaboré |
|
|
Le cobordisme et l'homotopie sont deux concepts
fondamentaux en topologie, mais ils abordent les relations entre les espaces
de manière différente.
|
Comparaison :
|
|
|
Présentation L’hypothèse du cobordisme affirme que pour
comprendre une théorie quantique topologique des
champs (TQFT), il suffit d’analyser ce qui se passe à l’échelle la
plus petite possible : un simple point. Tout le reste peut être construit à
partir de cette base. Cela a des implications profondes en
mathématiques et en physique, permettant aux chercheurs de mieux classifier
les théories et de comprendre la nature fondamentale de l’espace et du temps.
|
Analogie et application Prenons des cercles, des
sphères ou des surfaces plus compliquées. Certaines de ces formes
peuvent être transformées l’une dans l’autre en douceur, sans être coupées ni
recollées — c'est ce qu'on appelle le cobordisme. L’hypothèse affirme que
toute la structure d’une TQFT peut être déterminée uniquement à partir du
comportement d’un point. |
|
1.
Introduction
·
Objectif : L’hypothèse
du cobordisme est une idée qui relie des domaines aussi variés que
la topologie et la physique théorique. ·
Contexte :
Elle trouve notamment son application dans la construction et la
compréhension des théories quantiques topologiques des champs (TQFT). 2.
Concepts de Base
a. Topologie
·
Définition : La topologie
est l’étude des propriétés des espaces et des formes qui restent invariantes
malgré des déformations continues (sans déchirures ni collage). ·
Exemple : Un
cercle et une ellipse sont équivalents en topologie, car l’on peut
transformer l’un en l’autre par une déformation douce. b. Cobordisme
·
Définition simple :
Deux espaces (ou variétés) sont reliés par un cobordisme s'ils forment
ensemble la bordure d’un espace de dimension supérieure. ·
Illustration :
Imagine un cylindre dont les deux extrémités sont des cercles. Le cylindre
montre comment deux cercles sont reliés l’un à l’autre par un cobordisme. c. Hypothèse du Cobordisme
·
Principe clé :
L’hypothèse affirme que pour une théorie quantique topologique, connaître le
comportement de la théorie sur le cas le plus simple – un point
– permet de comprendre et de reconstruire toute la théorie sur des objets
plus complexes. ·
Analogie :
C’est comme connaître la recette de base pour créer une multitude de plats
différents – le point joue ici le rôle de l’ingrédient fondamental. 3.
Application en Physique
·
Théorie Quantique Topologique des
Champs (TQFT) : o En
TQFT, les variétés (les différents objets spatiaux) sont associées à des
états quantiques. o Un
cobordisme représente alors une transition entre ces états : c’est une
manière de décrire comment l’espace-temps évolue de façon continue. ·
Gluing ou collage : o Les
théories quantiques qui utilisent le cobordisme permettent de coller
des portions d’espace-temps les unes aux autres pour obtenir une vue globale
de l’évolution d’un système. ·
Implication pratique : o En
se concentrant sur ce qui se passe avec un point, les physiciens et
mathématiciens peuvent construire et classifier toute une panoplie de
phénomènes complexes dans l’univers, en se basant sur des principes vraiment
fondamentaux. 4.
Exemples et Analogies Simples
·
Exemple Concret : o Cas
du point : Imaginons que l'on connaisse parfaitement le comportement d’une
théorie sur un simple point; o Construction
: En utilisant les règles de gluing (le collage), tu peux étendre ce
comportement pour décrire la théorie sur des lignes, des cercles, ou même des
surfaces entières. ·
Analogie Culinaire : o Une
recette de base qui, une fois maîtrisée, nous permet de créer une variété de
plats en ajoutant différents ingrédients et techniques. Ici, le point est cet
ingrédient de base à partir duquel tout se construit. 5.
Conclusion
·
Résumé :
L’hypothèse du cobordisme établit que: la connaissance du comportement d’une
théorie sur le cas le plus élémentaire (un point) permet de déterminer toute
la structure de la théorie pour des objets plus sophistiqués. ·
Impact :
Cette approche offre un pont puissant entre la topologie et la physique,
permettant d’appréhender de manière globale des phénomènes complexes comme
l’évolution de l’espace-temps, sans se perdre dans les détails géométriques. |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |