|
Édition du: 30/08/2022 |
|
INDEX |
Topologie – Graphes |
|||||
![]()
|
Graphes ou Polygones RIGIGES Théorème et graphes de Laman
Comment
rigidifier une structure. Quelles sont les bases appliquées au triangle,
au carré
et aux autres polygones
? Sujet
appartenant au vaste domaine de la géométrie
discrète sous contrainte au service de la rigidité structurelle. Ses
applications sont nombreuses en mécanique, travaux publics, chimie, etc. Ces pages
constituent une introduction et abordent le sujet sur le plan du
divertissement, du défi. |
||
|
|
Sommaire de cette page >>> Treillis et ponts >>> Polygones rigidifiés >>> Théorème de Laman (ou de la rigidité) >>> Graphes de Laman pour P = {3, 4, 5, 6} >>> Quantité des
graphes de Laman >>> Construction des graphes de Laman >>> Sous-graphes rigides |
Débutants Glossaire |
Anglais: Geometric Constraint Systems
(GCS) / Braced polygons
|
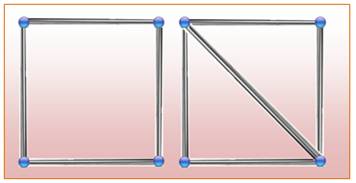
Rigide ou déformable Rendre
une structure indéformable consiste à créer des triangles, lesquels sont
indéformables. |
Un carré est
rigidifié en ajoutant une ferme en diagonale. |
|
|
Assemblage Un treillis, ou système triangulé, est un
assemblage de barres formant des triangles de sorte que la déformation de
l'ensemble soit nulle ou modérée. |
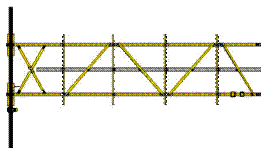
Treillis de grue
de chantier Truss of a crane
for construction site. |
|
|
Toit et pont Ferme de
toit (King post truss). Le treillis
le plus simple utilisé surtout pour supporter un toit ou renforcer un piquet
de clôture. Barre verticale maintenue en position par deux fermes latérales
obliques. La
seconde structure est plutôt destinée à la construction de pont Note Si l'intérieur du carré est haubané par deux
câbles d'acier (ou autres marériaux), c'est pour renforcer la solidité du
pont à la charge du trafic et non pour la rigidité. |
|
|
|
Treillis de Pratt Un des
treillis les plus simples, breveté en 1844 par Pratt et fils. Chaque rectangle est rendu rigide par une ferme
transversale. |
|
|
Voir La gamme des structures sur Treillis – Wikipédia
Tapez types de ponts haubanés ou types of truss bridges et
cliquez sur images
Exemples de ponts



|
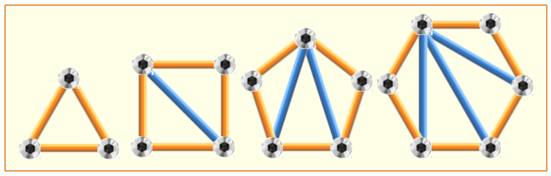
Création de triangles Pour rigidifier les polygones, il suffit d'ajouter des barres diagonales
pour diviser le polygone en triangles. |
Les fermes bleues sont alors de longueurs différentes de celles des
côtés. Un défi consiste à obtenir la rigidification en n'utilisant que des
barres de même longueur >>> |
||
|
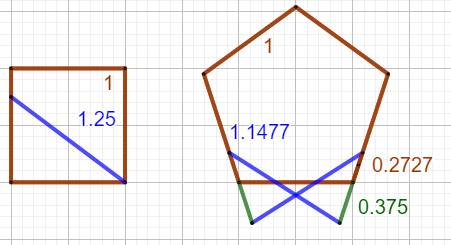
Maintien des angles Pour rigidifier le carré, il suffit de maintenir
un angle à 90°. Une équerre suffit. En l'occurrence la ferme bleue mesure 5/4, valeur
rationnelle. Avec le pentagone,
il faut maintenir deux angles fixes à 108°. Les fermes en croisillons font l'affaire et ont
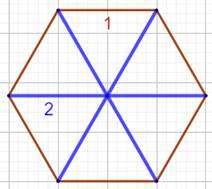
des dimensions rationnelles: Le cas de l'hexagone
est simple: trois barres de longueur double suffisent. Avec l'heptagone,
une solution originale utilise quatre barres de longueur unité et quatre
barres de longueurs 4/3 reposant au tiers des côtés. Un défi consiste à réaliser ces consolidations de
polygones avec des barres trouées régulièrement façon Meccano >>> |
|
||
Voir autres solutions en Rationally
bracing a rigid regular nonagon - Mathematics
|
Théorie des graphes Les graphes de Laman s'appliquent à des
structures rigides faites de barres et de joints (ou pivots). Le retrait d'une seule barre conduit à la
non-rigidité de la structure. On parle de graphe
structurellement bien contraint. Utile dans le domaine de la modélisation
géométrique par contraintes. Théorème décrit par Maxwell
(1831-1879) et démontré en 1970 par Gerard Laman (1924-2009). Propriété
connue d'Hilda Geiringer dès 1927. Un graphe rigide est aussi appelé graphe de Laman. Un tel graphe est caractérisé
par un invariant: 2P – A = 3. |
Théorème de Laman Un graphe 2D (cad. dans le plan), comportant A
arêtes et P pivots (ou points), est rigide:
A graph is generically,
minimally rigid in 2D if and only if it has 2n−3 edges and no subgraph
of k vertices has more than 2k−3 edges. Si A < 2P – 3, la quantité de déformations
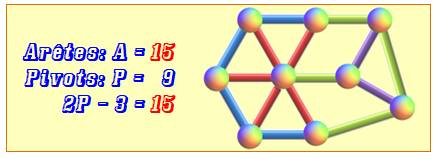
possibles est: Q = 2P – A – 3. Exemple de structure rigide selon
le théorème
|
|
|
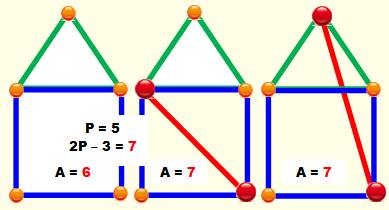
Cas de l'enveloppe La structure de gauche n'est pas rigide. Le
triangle est rigide, mais le carré peut se déformer. Une diagonale quelconque (rouge) assure la
rigidité. La quantité d'arêtes (7) est alors égale à 2P – 3
= 7. |
|
|
Voir Invariant
des polyèdres (Euler)
|
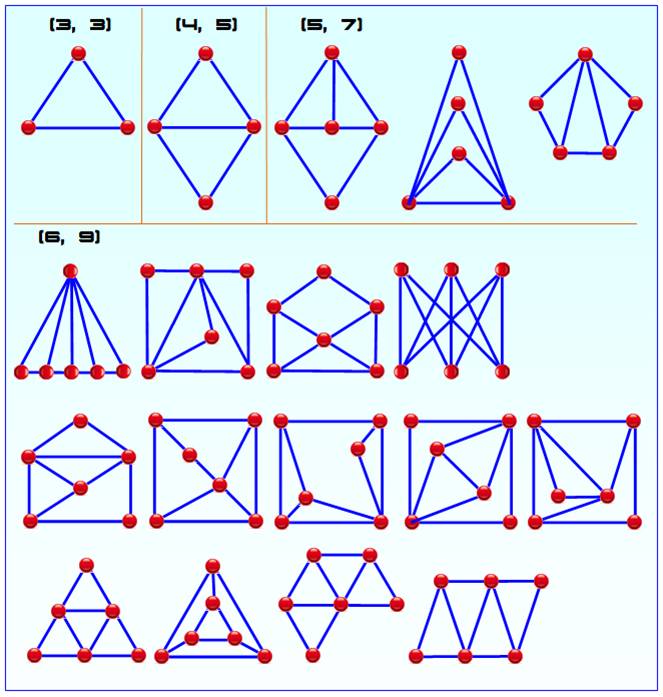
Tous les types de graphes de Laman pour P = {3, 4, 5, 6} |
||
|
D'après
Laman Graph –
Wolfram MathWorld Voir
Brève
de maths n° 564 |
||
|
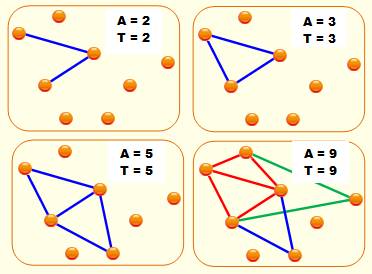
L'illustration indique la quantité de points (P), suivie de la
quantité d'arêtes (A). Ce graphique permet de compter les premières quantités
de graphes en fonction de P: (3 => 1); (4
=> 1); (5 => 3); (6 => 13). Dénombrement Le comptage des graphes de Laman
est extrêmement délicat. ll existe quelques algorithmes (peddle algorithm) exploitant
le théorème de Laman ou la méthode de construction de
Henneberg. Internet se fait l'écho de nombreuses études qui visent à
optimiser le temps de calcul. |
En partant de P = 0, la quantité de graphes de Laman est donnée par
cette suite: 1, 1, 1, 1, 3, 13,
70, 608, 7 222, 110 132, 2 039 273, 44 176 717, 1 092 493 042, 30 322 994 747, 932 701 249 291, … |
|
Voir OEIS A227117 – Number of minimally rigid graphs in 2D on n vertices
Aussi: OEIS
A306420 – Maximal Laman number among all
minimally rigid graphs on n vertices
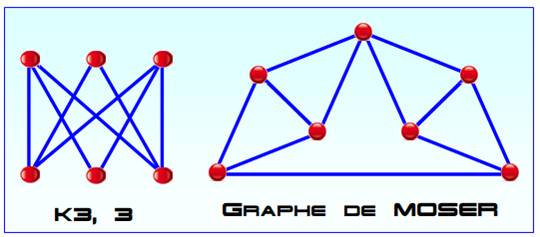
Voir Carré rigidifié
avec la structure de Moser / Gallery of named
graphs – Wkipedia
Anglais: Moser spindle ( broche de Moser)
|
Tous les graphes de Laman (graphes minimalement
rigides) avec P sommets peuvent être créés à partir Avec le premier type, un nouveau sommet est
ajouté au graphe et deux nouvelles arêtes sont créées, reliant le nouveau
sommet à deux sommets qui faisaient déjà partie du graphe. Avec le deuxième type de construction, une arête
S1 et S2 est supprimée. Un autre sommet S3
est sélectionné. Un sommet T est ajouté au graphe, ainsi que les trois arêtes
(S1, T), (S2, T) et (S3, T). Chacune de ces deux constructions ajoute
"1" à la quantité de sommets et "2" à la quantité
d'arêtes. Propriété: un graphe
construit en utilisant la construction de Henneberg est un graphe de Laman,
et tout graphe de Laman peut être construit avec la méthode de Henneberg. |
||
|
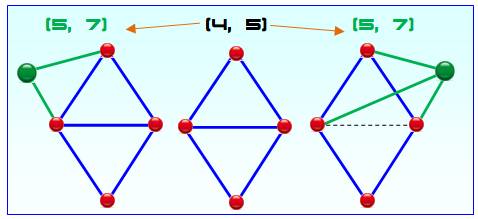
Exemple: passage du graphe à 4
points (sommets) aux trois graphes à 5 sommets À gauche, le graphe à 4 sommets auquel on ajoute
un sommet selon la méthode 1 (encadré rouge du haut), et selon la méthode 2
(encadré rouge du bas). Le nouveau sommet est ajouté soit à l'intérieur
soit à l'extérieur, deux cas considérés comme équivalents. Les arêtes joignent les sommets d'un côté (lignes
1 et 3) ou de la diagonale (lignes 2 et 4). À droite (encadré bleu), les trois types de
graphes à 5 sommets selon leur représentation dans le tableau ci-dessus. La colonne du centre montre les transformations
pour atteindre la représentation de droite. |
|
|
|
On se donne un tapis de P points quelconques et
on cherche la taille T du graphe rigide maximum réalisable avec A arêtes. Les
croisements sont autorisés. Lorsque P augmente, le tapis renferme d'abord et
surtout des graphes rigides de taille 2, et brusquement se met à présenter
des graphes rigides de grande taille. Une sorte de polymérisation, de
transition de phases nommée percolation de la
rigidité. On a démontré que si:
Le rapport devient 3,588 pour des graphes rigides
limité au segment. |
Effet de
percolation étudié par P. Duxbury, C. Moukarzel, D. Jacobs, M. Thorpe, et
démontré en 2011 par S.P. Kasiviswanathan C. Moore et L. Théran. |
|
Pour plus d'informations, lire le document
du CNRS
Note: tenségrité en architecture
|
Tenségrité:
faculté d'une structure à se stabiliser par le jeu des forces de tension et
de compression qui s'y répartissent et s'y équilibrent. Les
structures établies par la tenségrité sont donc stabilisées, non par la
résistance de chacun de leurs constituants mais par la répartition et
l'équilibre des contraintes mécaniques dans la totalité de la structure. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/Rigide.htm
|