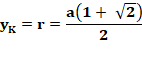NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 11/11/2020 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Polygone
Débutants Géométrie	OCTOGONE			Glossaire Géométrie
INDEX Polygones Géométrie	Général	Calculs	Octogone dans le parallélogramme
		Sommaire de cette page >>> Frise d'octogones >>> Diagonales de l'octogone – Calcul des longueurs >>> Coordonnées des sommets de l'octogone >>> Octogone et deux triangles équilatéraux >>> Constructions avec l'octogone et le carré >>> Octogone et ses cousins polygones >>> Constructions avec l'octogone et le carré

OCTOGONE – Calculs et curiosités

Calcul des coordonnées des sommets.

Propriétés avancées: démontrez que deux triangles équilatéraux possèdent un point commun: usage de la géométrie analytique et de la trigonométrie.

Frise d'octogones

Octogone régulier et ses diagonales

Longueur de la diagonale k, avec k la quantité de côtés interceptés par la diagonale.

k	Longueur	Formule
2	1,847759064
3	2,414213561
4	2,613125929

Voir Son calcul / Tables / Quantité d'intersections des diagonales

Diagonales de l'octogone – Calcul des longueurs
Exercice de géométrie Angle au sommet interceptant un côté Diagonales d1 = AE = D d2 = AD= BE = 2MK = 2r d3 = AC Rayon des cercles circonscrit: MA = R = D/2 inscrit: MK = r Apothème MK = BE/2 = r Calculs des longueurs pour une longueur du côté: a = 10.
Grande diagonale, diamètre du cercle circonscrit (D): d1 = AE
Deuxième diagonale, diamètre du cercle inscrit, 2 x apothème: d2 = 2r = EB
Petite diagonale d3 = AC:

Coordonnées des sommets de l'octogone
Octogone inscrit dans un cercle de rayon r = 10; alors a = 8,284271248… Coordonnées des sommets par rapport au centre 0 Lignes trigonométriques des angles

Voir Trigonométrie –Tables / Angles en Pi/8 / Tangente Pi/8

Octogone et deux triangles équilatéraux
Données Un octogone régulier ABC…H. Un petit triangle équilatéral sur le côté GH. Un grand triangle équilatéral sur la corde AC. Question Le point K étant le sommet du petit triangle, montrez qu'il est situé sur un côté du grand triangle. K est sur la droite AJ. Principe Calculer la tangente de l'angle JAB et la tangente de l'angle KAB et constater l'égalité. Calcul
Tangente de l'angle JAB = 82,5°
Coordonnées du point K par rapport à l'origine A
Tangente de l'angle KAB
Image construite avec Geogebra Notez la symétrie et la présence de deux sommets sur le triangle équilatéral bleu.

Voir Triangles équilatéraux dans le dodécagone / Généralisation au cercle

Octogone et ses cousins polygones
Un octogone régulier et tous les autres polygones réguliers construits sur une de ses bases. Comparaison aux sommets des triangles équilatéraux construits sur les côtés. Points remarquables Les deux points roses, sommets des triangles équilatéraux sont effectivement sur les côtés du carré surmonté d'un triangle équilatéral.
Mais, le sommet du triangle équilatéral supérieur (point rouge) n'est pas le sommet supérieur du pentagone (croix verte), comme le montre cet agrandissement.		Valeurs relevées (n est le côté) Écart: 0,935%

Voir Construction étonnante du pentagone

Merci à Jean-Louis Breuil pour son travail présenté en annexe

à l'origine de la rédaction de cette page.

Voir également: Étude de la généralisation au cercle par le même auteur

Constructions avec l'octogone et le carré – Amusements

À gauche: octogone régulier (angles: 135°) / À droite: octogone particulier (angles: 120° et 150°)

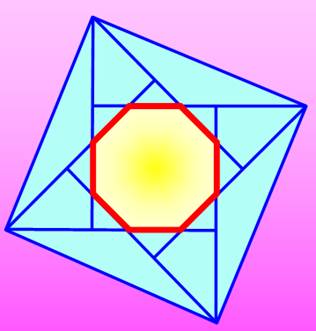
Voir Carré et triangles équilatéraux

Rosace avec octogones

Retour	Octogone – Approche
Suite	Octogone semi-régulier Octogone dans le parallélogramme Culture 8 Ennéagone Décagone Polygone – Index
Voir	Angles – Index Construction géométrique des nombres Géométrie – Index Trigonométrie – Index
DicoNombre	Nombre 8
Cette page	http://villemin.gerard.free.fr/GeomLAV/Polygone/Octogon1.htm