|
Édition du: 06/06/2025 |
|
INDEX |
Polygones – Partages |
|
|
Partage par les diagonales
(Hexagone) |
||
Faites un double-clic pour un retour en haut de page
Tout
sur l'heptagone
![]()
|
Dissection de l'heptagone
Sujet: dissections de l'heptagone
régulier avec ses diagonales sans intersection en triangles et quadrilatères. Décompte: 154 dissections
avec triangles et quadrilatères dont la décomposition est indiquée dans le
tableau. |
||
|
|
Sommaire de cette page >>> Dissection de l'heptagone >>> Dénombrement des dissections de l'heptagone >>> Heptagone et une diagonale >>> Heptagone et deux ou trois diagonales >>> Heptagone et cinq diagonales >>> Heptagone: 1 quadrilatère et 3 triangles |
Débutants Glossaire |
Exemple
de dissections de l'heptagone par ses diagonales
avec
formation d'un quadrilatère et de trois triangles

|
Dissection Il
s'agit ici du partage de l'heptagone par ses diagonales non-sécantes. Il
en résulte la formation de "sous-polygones" en nombres précis. Six types de dissections L'heptagone
comprenant sept côtés, il est partagé au plus par quatre diagonales qui forment
5 triangles. Les
autres dissections sont obtenues en supprimant les diagonales une à une. La
table montre la transformation des triangles (T) en autres polygones:
quadrilatère (Q), pentagone (P) et hexagone (H) . La
figure illustre ces six cas de dissections. Formule Notez
que la quantité T de triangles vaut 5, soit 2 de moins que N, le nombre de
côtés. Ensuite,
on déduit qu'un quadrilatère Q vaut 2T; un pentagone = 3T et un hexagone =
4T. D'où
la formule générale pour tout polygone: T +
2Q + 3P + 4H = N – 2 Combien de dissections ? L'enjeu
consiste à dénombrer toutes les dissections possibles pour chaque type et
cela en considérant toutes les combinaisons des diagonales. |
Type de dissections de l'heptagone
Illustration des six types
|
|
|
Le
tableau indique la quantité de dissections de l'heptagone selon les types de
dissections. Il
existe N = 203 dissections de tout type. Il
en existe N' = 154 pour toutes les dissections
réalisées par des triangles et/ou des quadrilatères. OEIS A001002 Il
en existe 42 pour les dissections avec seulement des triangles: nombres
de Catalan. |
|
|
![]()
Détails du dénombrement
|
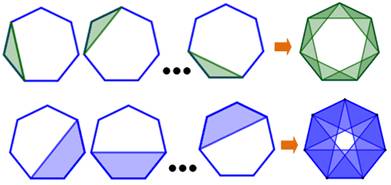
Avec
une seule diagonale, deux possibilités: Cas1: 1
hexagone et 1 triangle. La diagonale peut prendre sept positions, soit sept
dissections. Cas2: 1 pentagone
et un quadrilatère. Même chose: la diagonale peut prendre sept positions
créant sept dissections distinctes. |
Sept cas avec hexagone et sept autres avec pentagones
|
|
|
Cas1: deux
diagonales: |
Cas2: trois
diagonales: |
|
|
Cas 1: Vingt-huit dissections avec 2 triangles et 1 pentagone
|
||
|
Cas 2: Trente-cinq dissections avec 3 triangles et 1
quadrilatère
|
||
|
Avec
cinq diagonales, il s'agit de la triangulation
de l'heptagone. Elle est bien connue. La quantité de dissection est égale
à un nombre de Catalan.
|
Nombres de Catalan Rang
selon le nombre de côtés – 2 Soit
pour l'heptagone, le rang 5. 1,
2, 5, 14, 42,
132, 429, … |
|
|
|
||
|
Méthode utilisée Point de départ: les 42 partitions de l'heptagone
en triangles. Pour chaque cas, on supprime une diagonale
réunissant ainsi deux triangles en un quadrilatère. Le même quadrilatère peut être atteint de deux
façons par suppression de l'une ou de l'autre des diagonales. Le cas
redondant est marqué en ocre. Trapèzes latéraux (illustration) On compte 7 trapèzes identiques avec rotation de
1/7 de tour (7 lignes en blanc et 7 lignes en ocre pour les redondances). Chacun des trapèzes (ligne) est accompagné de 5
types (colonne) de répartition des triangles. Total: 35 |
|
|
|
Trapèzes isocèles On compte 7 trapèzes identiques avec rotation de
1/7 de tour. Chacun avec deux modèles de découpe en triangles. Total: 17 |
|
|
|
Trapèzes isocèles (suite) On compte 7 trapèzes identiques avec rotation de
1/7 de tour. Chacun avec deux modèles de découpe en triangles. Total: 7 |
|
|
|
Cerfs-volants On compte 7 lignes de quatre dissections,
accompagnées de leurs redondances Total: 28 Total des dissections avec 1
quadrilatère et 3 triangles 35 17 7 28 84 au
total |
|
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/Heptagon.htm
|