|
Édition du: 01/04/2023 |
|
INDEX |
Dénombrements - MOTIFS |
|||||
|
Nombres de
Catalan – Développements |
||||||
Faites
un double-clic pour un retour en haut de
page
![]()
|
NOMBRES DE CATALAN & Polygones Les
nombres de Catalan sont présents dans la triangulation des polygones
convexes. Combien
peut-on dessiner de triangles dans un pentagone ? La quantité de triangles dans un polygone convexe à n+2 côtés et n–1 diagonales non concourantes est égale au nombre de Catalan de rang n. |
||
|
|
Sommaire de cette page >>>
Triangulation du polygone convexe >>> Partage
des POLYGONES >>>
Euler et les polygones |
Débutants Glossaire |
Anglais : Catalan Numbers

|
T3
= 1 = C1 T4 =
2 = C2 T5 = 5
= C3 T6 = 14 =
C4 Tn+2 =
Cn |
Voir Brève
49-971
|
Combien de
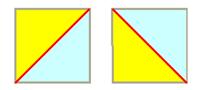
manières y a t'il de couper un polygone en triangles ? Carré On compte toutes
les possibilités pour le carré: |
|
|||
|
Pentagone Cinq façons de
couper le pentagone convexe en
triangles. |
|
|||
|
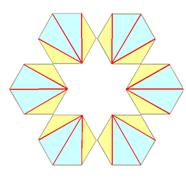
Hexagone Deux en
triangle, Soit 14 façons
de couper un hexagone
convexe en triangles. |
|
|||
|
Heptagone Il ya 42 = 6 × 7 façons de
couper un heptagone
convexe en triangles. Chacune des six configurations
de base produisent sept motifs par rotation. Pour les quatre
en bas, celle de gauche est la réflexion miroir de celle de droite
(symétrique). Les
42 triangulations de l'heptagone
|
|
|||
|
Euler découvre les nombres de Catalan en
répondant à question suivante: combien de façons de découper un polygone
convexe en triangles en dessinant des diagonales qui ne se coupent pas ? Le nombre de diagonales est n – 3 et le nombre de triangles n – 2 Le nombre
de triangulations des polygones sont les nombres de Catalan |
Euler prétend avoir eu du mal à trouver cette
formule, avec n la quantité de côtés:
Exemple pour l'hexagone
|
|
Triangulation du polygone et arbre binaire
|
Polygone, ici, à 13 côtés. Un des triangles est pris comme origine ou racine. Un point rouge identifie chacun des triangles (un point interne
quelconque). À partir de la racine, les paires de sommets connexes sont reliés.
La figure de gauche reprend l'arbre de
gauche en le rectifiant. |
Source images: Stanley
![]()
|
Suite |
||
|
Voir |
|
|
|
Livre |
|
|
|
Sites |
|
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPDENOM/Catalan/CataPoly.htm
|
|
![]()