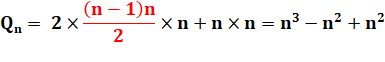Triangles dans la figure

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/04/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités				Glossaire Triangle
INDEX Types de triangles Triangle Dénombrement	Point Milieu	Droites et points	Pappus	Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli	Triangles et triangles
	Triangulation	Quatre triangles	Heilbron	Carrés triangles
		Représentation	Brocard	Cercles et triangles
		Triangles dans les polygones		Démo fallacieuse
		Sommaire de cette page >>> Les trois méthodes – Triangles dans le triangle >>> Bilan – Quand utiliser une méthode ou l'autre >>> Compter les triangles dans une figure complexe >>> Méthode générale sur cet exemple >>> Vérification

NOMBRES de TRIANGLES

dans un triangle ou dans une figure géométrique quelconque

Exposé de trois méthodes permettant de compter la quantité de triangles dans un dessin; de la méthode la plus simple à celle qui résout le cas général; avec exemples.

Devinette

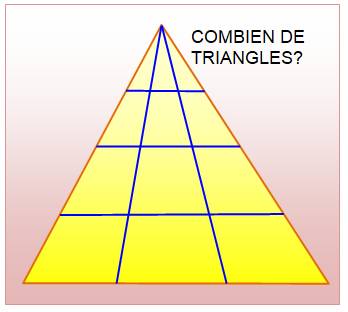
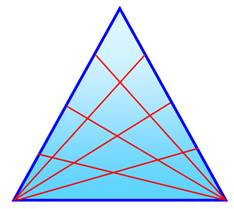
Il s'agit de dire combien de triangles vous compter sur cette figure, sans en oublier un seul. Soyez méticuleux pour compter …

La plupart des gens disent 24. Est-ce votre avis également ?

Attention ! Sans une astuce ça ne serait pas drôle.

Solution

Les trois méthodes – Triangles dans le triangle
Problème Combien de triangles dans cette figure ? Notez pour la suite que les côtés du triangle isocèle sont découpés en deux segments
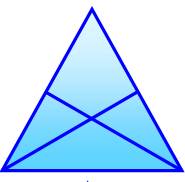
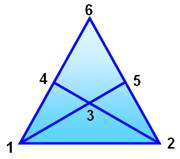
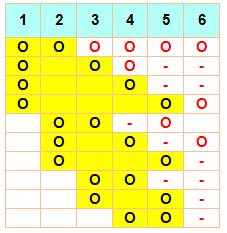
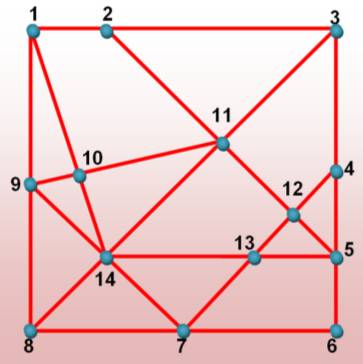
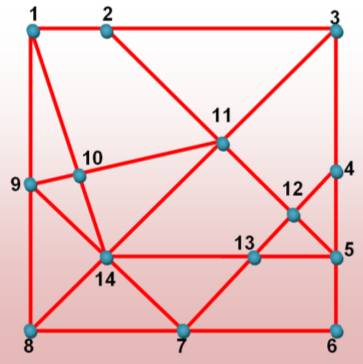
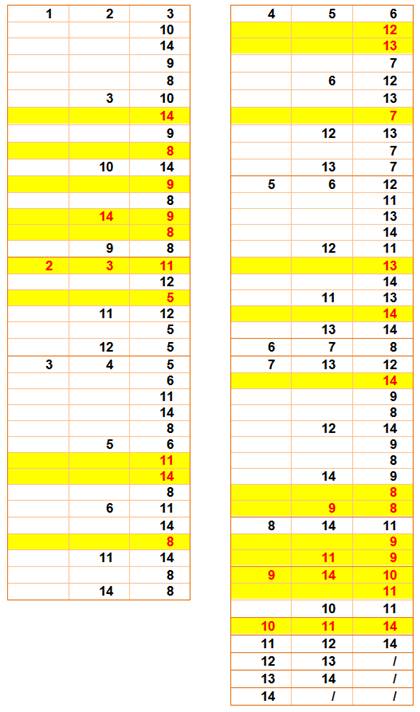
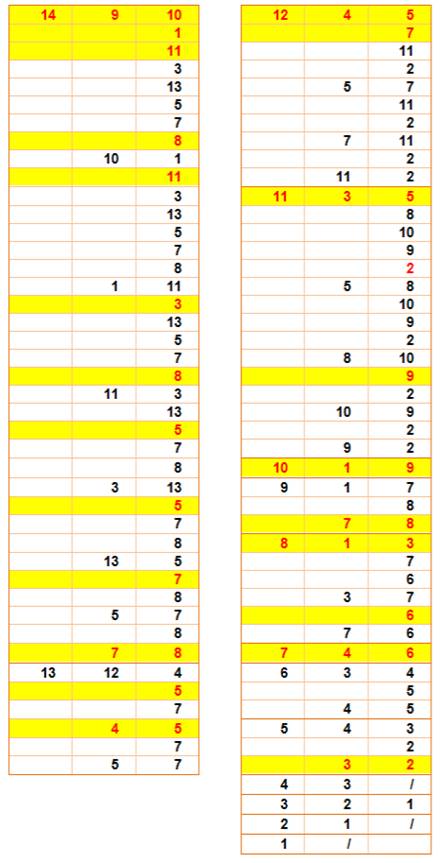
Méthode 1 – Comptage En comptant simplement, on en dénombre (en jaune): 1 + 2 + 2 + 1 + 2 = 8 triangles Notez que: 8 = 2³. Astuce de comptage: si un triangle de taille k contient k surfaces individuelles, alors il y a: k = 1 => 3 triangles k = 2 => 4 triangles k = 4 => 1 triangle; total 8.
Méthode 2 – Dénombrement par grille Avec une méthode systématique, impossible d'en oublier. En jaune avec deux ronds: tous les segments possibles; En rouge, un rond chaque fois que le sommet forme un triangle avec le segment de la ligne. Ex: 123, 124, 125, … 134 … 156 …	Les numéros sont ceux des sommets ou des intersections.

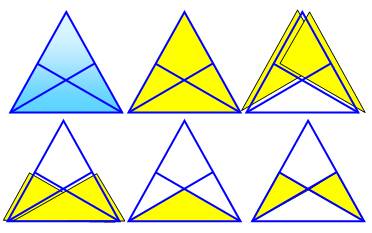
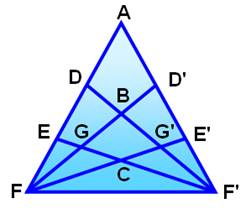
Méthode 3 – Sommets générateurs

Adaptée aux figures symétriques, mais atention aux doublons.

Quantité de triangles:

2 x (3 x 3) + (3 x 3) = 27 = 3³

ANGLE en F

Angle AFF': FEF', FDF', FAF'

Angle AFE': FEC, FDG', FAE'

Angle D'FF': FGF', FBF', FD'F'

Angle AFD': FEG, FDB, FAD'

Angle D'FE': FGC, FBG', FD'E'

Angle E'FF': FCF', FG'F', FE'F'

Il y a 18 triangles issus de F et autant issus de F' …

à l'exception des triangles qui sont vus à la fois par F et par F' (en rouge: ils ont FF' comme côté commun).

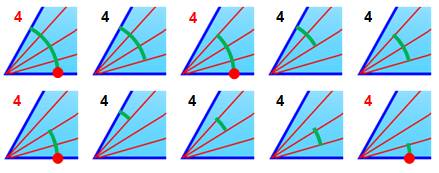
Méthode 3 en action

Sur la figure, on identifie les 10 sortes d'angles (arcs en vert):

Chaque angle engendre quatre triangles, d'où le nombre quatre indiqué. En doublant pour tenir compte de l'angle symétrique, on aurait: 2 x (10 x 4) = 80 triangles

Or, lorsque un côté de l'angle est la base (identifié par un point rouge), alors les triangles ne doivent être comptés qu'une seule fois.

Quantité de triangles:

2 x (6 x 4) + 4 x 4 = 64 = 4³

Pour ceux qui voudrait dénombrer visuellement, avec k la quantité q de surfaces dans chaque triangle, on a (q, k) =

(7, 1) (14, 2) (10, 3) (13, 4) (6, 6) (6, 8) (3, 9) (4, 12) et (1, 16).

Notez qu'avec les deux segments obliques du bas, on compte 3 + 1 + 3 = 7 triangles avec k = 1

=> (k, q) = (7, 1).

Généralisation

Avec ces deux exemples, on constate que la quantité (Q) de triangles est égale au cube du nombre de segments (n) découpés sur un côté .

Propriété vraie quel que soit n.

Q₄ = 2 x 6 x 4 + 4 x 4

La 6 résulte de: 1 pour les angles de 3 intervalles, 2 pour 2 intervalles, 3 pour 1 intervalle, soit 3 + 2 + 1. C'est la somme des entiers de 1 à 3.

Bilan

Cas simple => méthode 1 par comptage.

Cas d'une figure symétrique => méthode 3 par sommets générateurs de triangles.

Cas général => méthode 2 => par utilisation d'une grille de connexions.

Exemple complexe avec utilisation de la grille de connexion, ci-dessous.

Compter les triangles dans la figure proposée

Voici un dessin du type de ceux qui figurent dans des concours. Il s'agit de compter la quantité de triangles dessinés dans la figure. Comme (1, 9, 10), tout en excluant ceux que l'on pourrait dessiner (1, 2, 10).

Sauf pour les cracs, il est impossible de comptez de tête sans oublier un ou deux triangles, ou en compter en double.

Voyons une méthode systématique qui permet de les dénombrer à coup sûr.

Méthode systématique
La méthode consiste à examiner chaque point numéroté dans l'ordre croissant de 1 à 14; faire la liste de tous les points d'ordre supérieur au numéro courant qui lui sont réunis par un trait ignorer les points de numéro inférieur au numéro courant, car le triangle (1, 3, 8) est identique à (3, 1, 8) ou (8, 1, 3); composer toutes les combinaisons de trois des points de cette liste; détecter quelles sont les combinaisons décrivant un triangle; et compter ces combinaisons. L'aide d'un tableur comme ardoise est appréciable.
Exemple: Point 1, connecté à 2, 3, 10, 14, 9, 8. Triplets: (1 2 3, 1 2 10, 1 2 14, …) Triplets triangles (1 3 14, 1 3 8, 1 10 9, 1 14 9 et 1 14 8). Point 2, connecté à 3, 11, 12, 5. J'ignore le 1 déjà traité et je n'oublie pas les points alignés. Le tableur facile l'écriture. Le décompte demande beaucoup de soin.	TOTAL : 23 triangles

Voir Méthode améliorée appliquée aux polygones

Vérification

Si l'enjeu est important, n'hésitez pas à refaire le décompte en prenant les numéros de points à l'envers.

Une fois l'exercice terminé, vérifiez que les triangles identifiés ici sont bien ceux de là-haut. Pour cela, je marque en rouge les configurations identiques.

Cette vérification est surtout utile si vous ne trouvez pas la même quantité de triangles dans les deux cas.