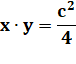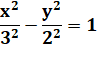Types d'hyperboles

Étymologie: Le mot hyperbole vient du latin hyperbole, du grec: hyperbolë, excès exagération; composé de hyper, au-delà et ballô, jeter, lancer

Sommaire de cette page

>>> Hyperboles en 1/x

>>> Notations – Fonction inverse

>>> Hyperbole équilatère

>>> Hyperboles avec équation standard

>>> Hyperboles avec équation homographique

>>> Hyperboles avec équation générale

>>> Hyperboles en pratique

>>> Anglais

Débutants

Géométrie

Glossaire

Géométrie

Hyperboles en 1/x

haut

Fonction inverse:

ou plus généralement

La fonction f(x) est indéfinie pour x = 0. >>>

Hyperbole

Cette hyperbole est équilatère (asymptotes orthogonales: ligne horizontale et ligne verticale).

Son excentricité vaut racine de 2.

Son équation peut aussi s'écrire:

Hyperbole avec la fonction inverse étendue

Graphe de la fonction inverse:

Notations mathématiques à propos de la fonction inverse

Voir Fonction homographique / Symboles mathématiques

Hyperbole équilatère		haut
Hyperbole équilatère ou rectangulaire Graphe de la fonction: L'angle entre asymptotes est 90° Exemple (Illustration)
Théorème de Brianchon-Poncelet Lorsqu'un triangle (bleu) est inscrit dans une hyperbole équilatère (rose), son orthocentre (vert) est aussi sur l'hyperbole.

Hyperboles avec équation standard		haut
Hyperbole générale Graphe de la fonction: Exemple (Illustration) Suite >>>
Propriété Soit au moins deux sécante parallèles; les milieux des cordes interceptées. Une droite passe par tous ces points et le centre.

Hyperboles avec équation homographique

haut

Hyperbole homographique

Graphe de la fonction homographique:

Exemple

Fonction homographique

Quotient de deux polynômes du premier degré.

Suite >>>

Hyperboles avec équation générale		haut
Hyperbole équation générale Exemple
Équation générale des coniques Devient hyperbole si: ac – b² < 0 Équilatère si a = - c Exemple

Hyperboles en pratique		haut
Miroir parabolique Tout rayon projeté sur une branche de l'hyperbole est réfléchit et se dirige vers le foyer opposé. Utilisation dans les télescopes associés à des miroirs paraboliques.
Navigation LORAN (Long Range Navigation) Ondes terrestres émises par deux émetteurs, utilisées par les navires pour déterminer leur position: mesure de la différence de temps de propagation.
Mur du son Un avion en vitesse supersonique crée une onde sonore, un cône sonore. Son impact au sol dessine une hyperbole. La zone rectangulaire au sol où le bang sonore est le plus audible a une largeur d'environ cinq fois l'altitude de l'avion.	Source image: Wikipedia
Trajectoire d'un engin spatial passant à côté d'un astre avec effet catapulte. L'engin s'approche à une vitesse V et s'en éloigne à une vitesse plus grande.
Tour de réfrigération utilisée notamment dans la centrale nucléaire a la forme d'une hyperbole. La forme hyperbolique augmente le débit d'air et améliore la portance aérodynamique due au vent qui la traverse. La forme hyperbolique de cette tour de refroidissement offre une résistance supérieure de sorte que moins de matériaux sont nécessaires lors de sa construction.
Tour de Kobe – Japon (Kobe Port Tower) Structure hyperboloïde. La tour de Kobe est une plateforme d’observation panoramique située dans le parc Meriken, au bord de la baie d’Osaka. Inaugurée en 1963, sa structure hyperboloïde d’une hauteur de 108 mètres est devenue au fil du temps le symbole de la ville.
Guitare Ses flancs sont en forme d'hyperbole. Forme qui facilite la prise en main. Abat-jours avec forme hyperbolique pour uen meilleure diffusion de la lumière.
Engrenage hypoïde Structure en hyperboloïde de révolution Utilisation dans l'automobile. Ils permettent d'avoir un renvoi d'angle ainsi qu'un rapport de réduction plus grand que les engrenages coniques.

Anglais

Hyperbola in a Cartesian Plane

Hyperbola: the set of all points in a plane such that the difference in the distances between two fixed points, called foci, is constant.

The middle of the segment that joins the foci is the centre of the hyperbola.

The line which passes through the two foci is the transverse axis and the line that passes through the centre, and that is perpendicular to the transverse axis, is the conjugate axis.

The basic equation of the relation which defines a hyperbola in a Cartesian plane is x²/a² - y²/b² = 1, where a is the length of the semi-transverse axis and b is the length of the semi-conjugate axis.

The points with coordinates F₁(−c, 0) or F₂(c, 0), where c² = a² + b², are the foci of the hyperbola.

The hyperbola is equilateral when a = b, that is to say when the asymptotes are perpendicular.

Voir Anglais pour le bac et pour les affaires

Haut de page

Retour	Coniques
Suite	Fonctions hyperboliques Parabole Cubique d'Agnesi Trigonométrie hyperbolique
Voir	Cercle Cône Courbes élémentaires DicoMot Ellipse Fractions unitaires Fractions égyptiennes	Géométrie – Débutants Géométrie – Glossaire Géométrie – Index Inverse d'un nombre Sphère Théorème de Pascal
Sites	How to construct a hyperbola – GeoGebra – Irina Boyadzhiev – Animation Hyperbola – Math is Fun
Cette page	http://villemin.gerard.free.fr/Geometri/Coniques/HyperTyp.htm