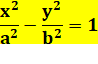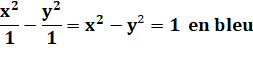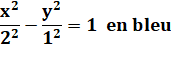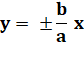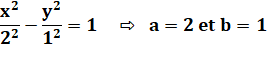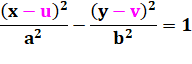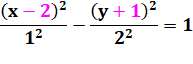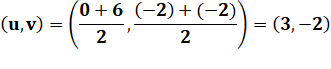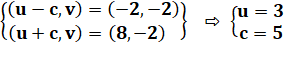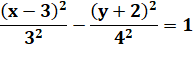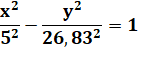|
Édition du: 27/02/2021 |
Pages sur l'hyperbole
![]()
|
Hyperbole standard L'hyperbole
est une courbe plane de la famille des coniques. Elle
possède deux asymptotes. Équation
standard de l'hyperbole:
Changer le signe
moins en signe plus et on obtient une ellipse. Étymologie: Le mot hyperbole vient du latin hyperbole, du grec: hyperbolë, excès exagération; composé
de hyper, au-delà et ballô, jeter, lancer |
||
|
|
Sommaire de cette page >>> Formulaire de l'hyperbole standard
>>> Géométrie –
Définition de l'hyperbole >>> Paramètres de
l'hyperbole centrée >>> Paramètres de
l'hyperbole non-centrée >>> Dessin rapide
d'une hyperbole >>> Calcul de
l'équation de l'hyperbole >>>
Établissement de l'équation >>> Propriétés –
Trigonométries >>> Directrices et
excentricité |
Débutants Glossaire |
Humour
|
HYPERBOL: chance démesurément insolente – Pascal Légitimus |
Voir Pensées et Humour
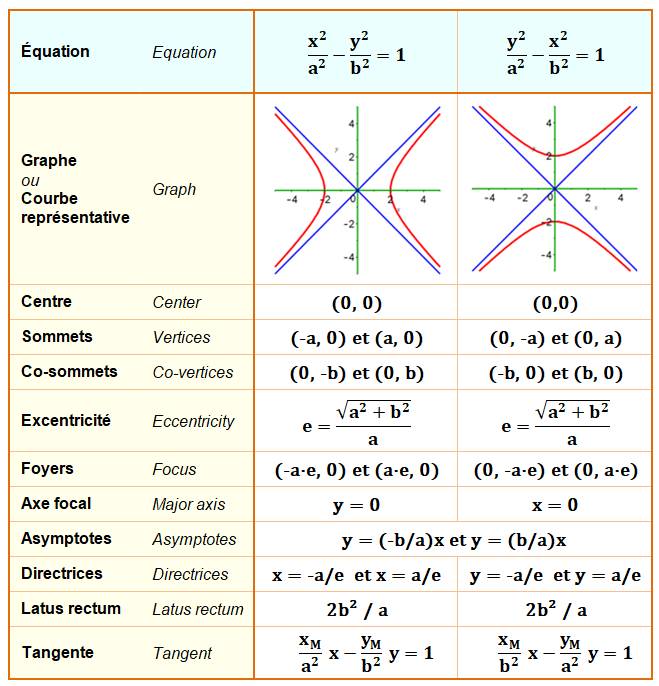
Formulaire de
l'hyperbole standard
![]()
|
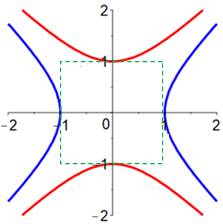
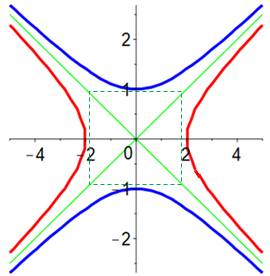
Équation de cette hyperbole avec a = b = 1:
Dimensions du carré vert en pointillé: Lx = 2a = 2 et Ly = 2b = 2 |
|
|
|
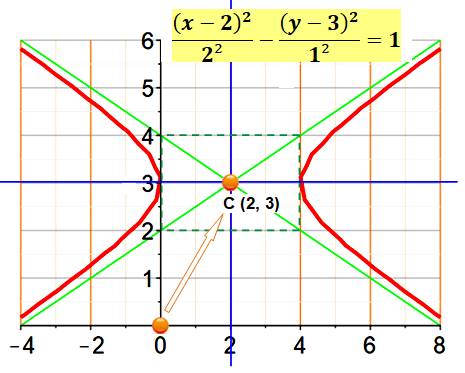
Équation de cette hyperbole avec a = 2 et b = 1:
Dimensions du rectangle vert en pointillé: Lx = 2a = 4 et Ly = 2b
= 2 Équation des asymptotes (vertes):
|
|
|
|
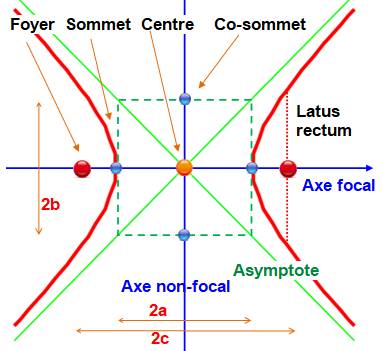
Hyperbole:
une courbe plane composée de deux branches disjointes et symétriques. Elle est caractérisée
par:
Latus rectum: corde au foyer
et perpendiculaire à l'axe focal. |
|
|
|
Équation de l'hyperbole Coordonnées du centre: (0, 0) Coordonnées des sommets: (-a, 0) et (a, 0) Coordonnées des foyers: (-c, 0) et (c, 0) Caractérisation de l'hyperbole
Distance entre foyers telle que: Équations des asymptotes Angle entre asymptotes
|
Calcul de la position du foyer –
Exemple
Valeur de b avec a et c
|
|
|
Équation de l'hyperbole Centre: (u, v) Sommets: (u – a, v) et (u + a, v) Foyers: (u – c, v) et (u + c, v) Caractérisation de l'hyperbole
Distance entre foyers telle que: Équations des asymptotes Angle entre asymptotes
|
L'hyperbole est simplement translatée de u = 2 en
horizontal et de v = 3 en vertical. |
|
Dessin rapide d'une hyperbole non-centrée
|
Exemple
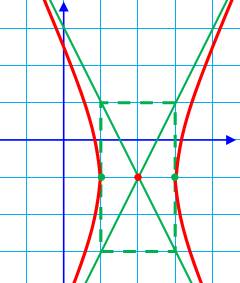
Centre (2, -1) a = 1 et b = 2 Construction Positionner le centre
(rouge) en (2, -1) Positionner les sommets
(verts) à une distance horizontale de a = 1 du centre. Dessiner le rectangle
(pointillé vert) de dimension (2a = 2 et 2b = 2 x2 = 4), centré sur le
centre. Tracer les droites
diagonales du rectangle (vertes). Ajuster les courbes rouges
pour qu'elles passent par les sommets et qu'elles s'approchent
progressivement des asymptotes. |
Comment construire une hyperbole approchée, mais
bien positionnée
|
|
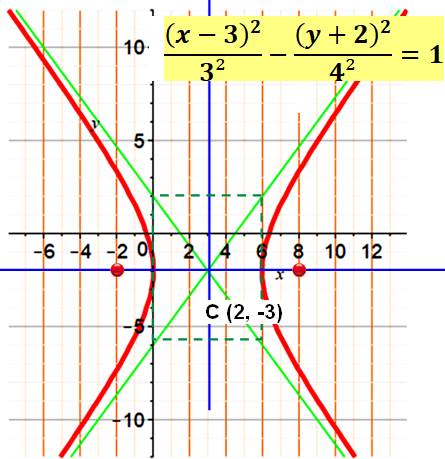
Exemple 1 |
Avec sommets en (0, -2) et (6,
-2) et foyers en (-2, -2) et (8, -2) |
|
|
Le centre subit la translation |
|
|
|
Distance entre sommets |
|
|
|
Avec coordonnées des foyers Résolution du système d'équations |
|
|
|
Calcul de b |
|
|
|
Équation de l'hyperbole |
|
|
|
Graphe Angle entre asymptotes, embrassant l'hyperbole: |
|
|
|
Exemple 2 |
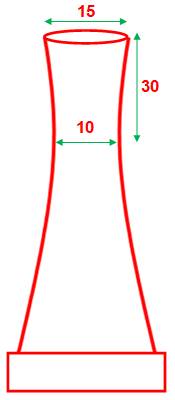
Tour de refroidissement d'une centrale électrique. Unités en mètres. |
|
|
Centre des axes |
Milieu de la flèche verte (10) qui est la distance la plus courte
entre les deux branches. |
|
|
Distance entre sommets: |
|
|
|
Point de l'hyperbole |
M (7,5 ; 30) |
|
|
Dans l'équation |
|
|
|
Calcul de b |
|
|
|
Équation de l'hyperbole |
|
|
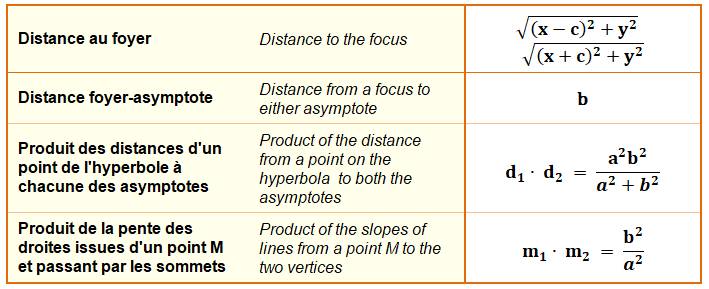
Distance au foyer |
|
|
|
Différence constante, égale à 2a |
|
|
|
Mise au carré après passage d'un radical à droite |
|
|
|
Radical isolé et développement des carrés; puis division par 4 |
|
|
|
Élévation au carré |
|
|
|
Variable x d'un seul côté |
|
|
|
Factorisation |
|
|
|
Or b² = c² – a² |
|
|
|
Division par a²b² |
|
|
|
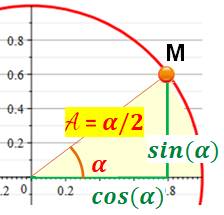
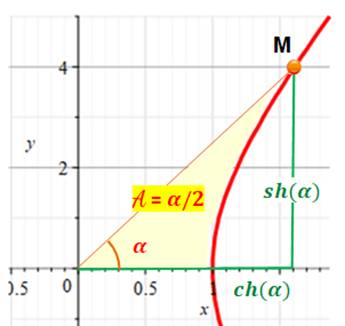
Analogie Cercle / Hyperbole Cercle de rayon 1 et hyperbole avec a = 1:
Avec un angle alpha dans les deux cas:
|
|
|
|
L'hyperbole peut aussi être définie comme le lieu
des points tels que:
Ces deux rapports sont constants et égaux à e, l'excentricité. Les deux droites bleues sont les directrices qui ont pour équations: La bissectrice de l'angle F1MF2
(droite en petits pointillés) est aussi la tangente
en M à l'hyperbole. |
|
|
![]()
|
Retour |
||
|
Suite |
||
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
http://villemin.gerard.free.fr/Geometri/Coniques/Hyperbol.htm |
|