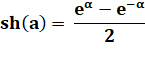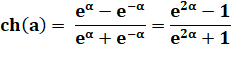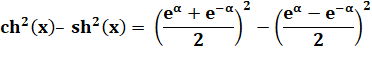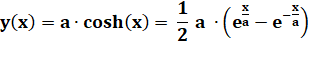|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Trigonométrie hyperbolique On connait la trigonométrie classique basée sur
l'utilisation d'un cercle
unité. La trigonométrie hyperbolique est similaire, mais basée
sur l'hyperbole.
|
|
|
||
|
Nous
connaissons la trigonométrie classique dite circulaire. Il existe
un autre type de trigonométrie, bâtie sur le même modèle, mais à partir de
l'hyperbole. Voyez et
comparez ces deux illustrations. Analogie Cercle / Hyperbole Cercle
de rayon 1 et
Pour un point M, avec un angle alpha dans les
deux cas:
|
|
|
Notations
|
sinus hyperbolique |
sinh |
sh |
|
cosinus hyperbolique |
cosh |
ch |
|
tangente hyperbolique |
tanh |
th |
|
cotangente hyperbolique |
cotanh |
|
|
sécante hyperbolique |
sech |
|
|
cosécante hyperbolique |
cosech |
|
|
arc sinus hyperbolique |
asinh |
sinh-1 |
|
arc cosinus hyperbolique |
acosh |
cosh-1 |
|
|
||
|
Prenons
l'hyperbole centrée, avec a = b = 1: On se souvient que a et b déterminent
la taille du carré vert et la direction des asymptotes. |
|
|
|
Avec un
calcul à partir de l'aire du secteur d'hyperbole embrassé par l'angle alpha,
on établit les formules en exponentiel qui expriment les valeurs des lignes
trigonométriques hyperboliques. |
|
|
|
|
||
|
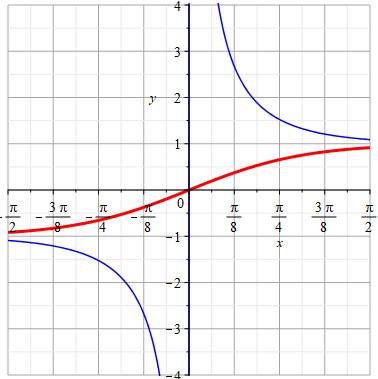
Sinus hyperbolique (rouge) Cosinus hyperbolique (bleu) de -Pi/2 à Pi/2
|
Idem de -3Pi/2 à
3Pi/2
|
|
|
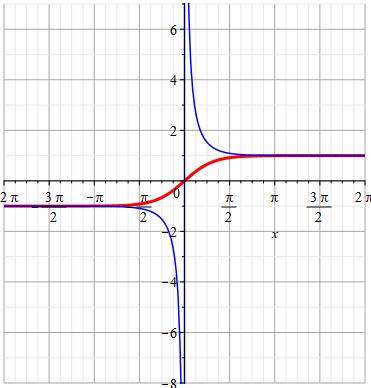
Tangente hyperbolique (rouge) Cotangente hyperbolique
(bleu) de -Pi/2 à Pi/2
|
Idem de -3Pi/2 à
3Pi/2
|
|
|
|
|||
|
Inverse |
sh (–x) = –sh(x) ch (–x) = ch(x) |
th (–x) = –th(x) coth (–x) = –coth(x) |
|
|
Différence |
ch (x) + sh (x) = ex
ch (x) – sh (x) = e-x |
ch² (x) – sh² (x) = 1 |
|
|
Somme |
sh (x + y) = sh (x) ch
(y) + ch (x) sh (y) ch (x + y) = ch (x) ch
(y) + sh (x) sh (y) sh (x – y) = sh (x) ch
(y) – ch (x) sh (y) ch (x – y) = ch (x) ch
(y) – sh (x) sh (y) |
||
Suite sur les sites Wikipédia >>>
Différence des carrés
|
Or: (a + b)² – (a – b )² =
4ab
|
|
|
||
|
Courbe
plane transcendante que prend un câble ou une chaine (catena) suependue à ses
extrémités et soumis à son propre poids.
|
|
|
![]()
|
Bases |
|
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/TriHyper.htm |
![]()