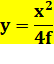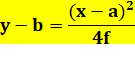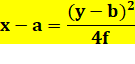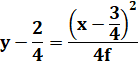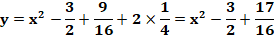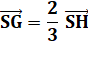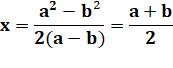|
||||||||||||||||||||||||||||||||
![]()
|
PARABOLE et PARABOLOÏDE
|
Parabole (allégorie)
|
Une parabole, du grec rapprochement, comparaison,
est une manière de communiquer un enseignement via une courte histoire qui utilise les
événements quotidiens. Les Évangiles en fait
un grand usage. |
|
Jésus: en vérité je vous me dis: y = x². Un apôtre: désolé, mais je n'ai pas compris! Jésus: normal, c'est une parabole! |
Voir Pensées & humour
|
|
||
|
Extremum
pour: – b / 2a
|
||
|
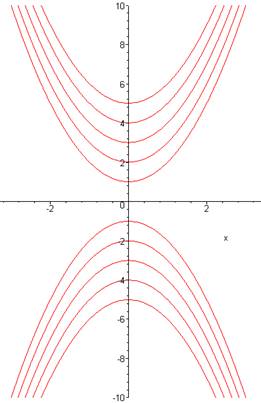
Effet du paramètre a Sur ces courbes a vaut successivement: 1, 2,
… 10, tandis que b et c son maintenus à 0.
La
parabole se referme lorsque a croît. |
Effet du paramètre c Sur ces courbes c vaut successivement: 1, 2,
3, 4, 5, tandis que a = 1 et b = 0.
La
parabole se relève lorsque c croît. |
|
Voir Magnifiques
illustrations de ces paramètres (Site Math is Fun)
|
|
||
|
Propriété fondamentale de la parabole La parabole est le lieu des
points tels que PF = PH; à égale distance d'un point F et d'une droite D.
|
|
|
|
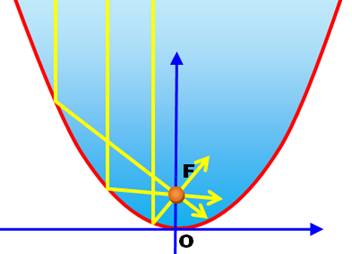
Propriété de convergence au foyer Toutes les droites
parallèles à l'axe se réfléchissent
sur la parabole et se
concentrent sur le foyer. Application pour concentrer les rayons
électromagnétiques des satellites (parabole de réception de la télévision ou
paraboles des radars). On trouve aussi cette forme dans les lampes torches
pour mieux concentrer les rayons lumineux. |
|
|
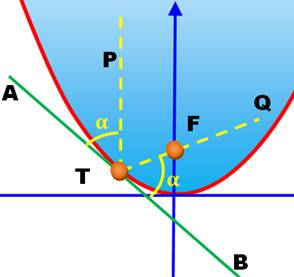
Propriété de réflexion La tangente AB en T à la
parabole. La parallèle PT à l'axe de
la parabole. Les angles alpha sont égaux:
Ce qui explique que tous les
rayons verticaux se réfléchissent au foyer. |
|
|
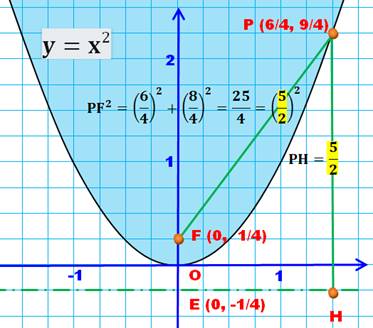
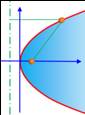
Parabole d'équation y = a x² avec a =
1. Son foyer est sur l'axe à l'ordonnée 1/4a = 1/4. Nous proposons de vérifier
cette propriété sur cette figure à l'échelle.
Nous retrouvons la propriété
fondamentale de la parabole: PF = PH. Démonstration |
|
|
|
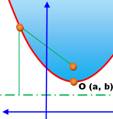
Prenons les notations
suivantes |
P (x, y)
et f la distance focale |
|
|
Exprimons les distances |
PH = PF
|
|
|
Élévation au carré |
y² + 2yf + f² = x² + y²
– 2yf + f² x² = 4yf |
|
|
Équation de la parabole
"verticale" |
|
|
|
Équation de la parabole
"verticale" avec sommet décalé: O (a, b) |
|
|
|
Équation de la parabole
"horizontale" |
|
|
|
|
||
|
Tentative avec le foyer Connaissant le sommet nous
savons que l'équation est de la forme suivante, mais sans connaître la
distance focale:
Recherche de l'équation avec les trois points Nous devons passer par la
résolution d'un système d'équations
à trois inconnues. Écrivons l'équation générique de la parabole pour les
trois points: P =>
11/4 = (9/4)²a + (9/4)b + c R => 6/4 = (7/4)²a + (7/4)b + c La résolution faite nous
donne les valeurs de a, b et c et, donc l'équation de la parabole:
|
Calcul de la distance focale En reprenant les termes des deux équations:
Nous vérifions que l'équation avec f devient:
|
|
![]()
|
Équation simple en
3D: z = x² + y² |
|
|
||
|
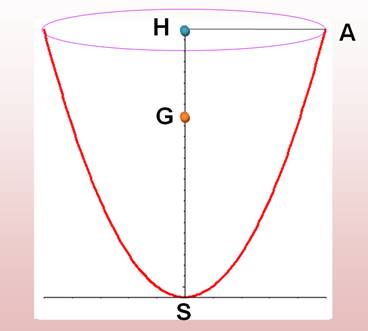
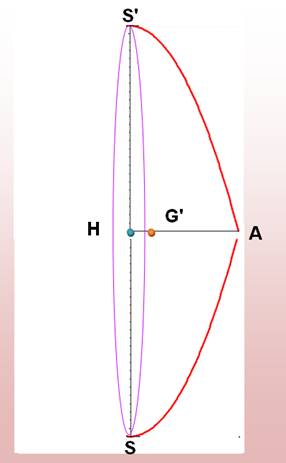
Paraboloïde L'arc de parabole SA est en rotation autour de SH. Le
volume engendré est un paraboloïde de révolution.
Le centre de gravité
du volume se situe au 2/3 de SH:
Résultat trouvé par Archimède, puis confirmé par Fermat. |
Conoïde L'arc de parabole AS est en rotation autour de AH. Le
volume engendré est un nouveau conoïde
de révolution selon le vocable de Fermat.
Le centre de gravité du volume se situe au 11/16 de AH:
En 1650, Fermat détermine également l'aire latérale du
conoïde. |
|
D'après Les Mathématiques, plaisir et nécessité
– Albert Ducrocq et André Warusfel – Vuibert – 2000
|
In the plane, fix both a line D and
a point F not on D. The collection of
all points P such that the length of
PD is equal to that of PF is called a parabola.
The line D is called the directrix and the
point F is called the focus. Yhe line through the focus that is
perpendicular to the directrix is the axis
of the parabola. The parabola is defined as the locus of a point which moves so that it is
always the same distance from a fixed point (called the focus) and a given
line (called the directrix). |
Voir Bagage
anglais
![]()
Niveau
avancé**
|
|
||
|
Propriété
Calcul |
|
|
|
Dérivée en A = pente en A |
p = 2k a |
|
|
Tangente en A: droite y = px + q |
y = 2k a x + q kxA² = 2k a a + q q = - ka² y = 2kax –ka² |
|
|
Équation de la tangente à la
parabole au point A: et pour B |
y = 2kax – ka² y = 2kbx – kb² |
|
|
Même ordonnée au point
d'intersection pour calculer x |
2kax – ka² = 2kbx –
kb² |
|
|
Et l'ordonnée y |
y = ka(a+b) – ka² = kab |
|
|
|
||
|
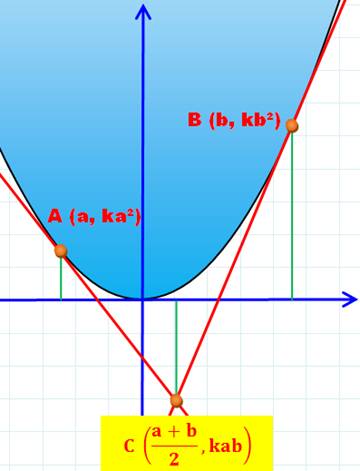
Deux points (A, B) quelconques sur la parabole et le milieu M du
segment AB. Propriétés
|
|
|
Voir explications
en Calcul du segment de parabole par
Archimède
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |
http://villemin.gerard.free.fr/Geometri/Coniques/Parabole.htm |
![]()