|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
ÉNIGMES sur les FAMILLES Suite |
|
Combien d'enfants ? |
|
|
|
Question Quinze
couples se retrouvent à la salle des fêtes. Un des
convives observateurs indique que les couples qui ont un seul enfant sont
aussi nombreux que ceux qui en ont cinq. Sinon, tous les autres couples ont
trois enfants. Combien
y-a-t'il d'enfants ? |
Réponse Inutile de recourir aux équations, un simple
échange fictif suffit. Les couples à cinq enfants en confient deux
momentanément aux couples à un enfant, transformant ainsi toutes ces familles
en couples à 3 enfants. Bilan, avec cette astuce, tous les couples ont
trois enfants, et le total est 15 x 3 = 45
enfants. Avec l'algèbre N = 15 = x + y + x = 2x
+ y E = x + 3y + 5x = 3 (2x
+ y) = 3 x 15 = 45 |
|
|
Généralisation avec 3 types de
couples Deux
conditions:
Généralisation avec 5 types de
couples Conditions:
|
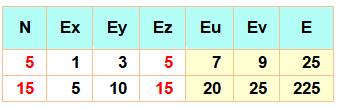
Exemples
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Famille |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()