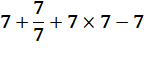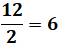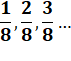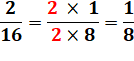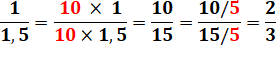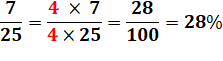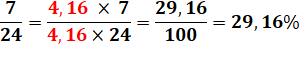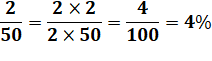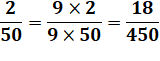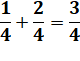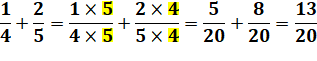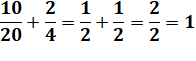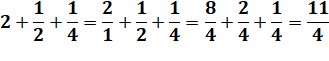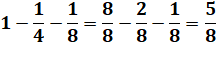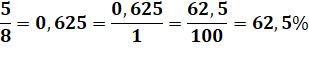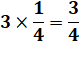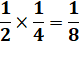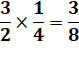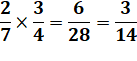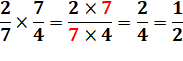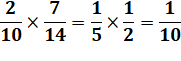|
|||||||||||||||||||||||||||||
![]()
|
Maths en 5e Revue des notions apprises
en 5e
|
|
|
||
|
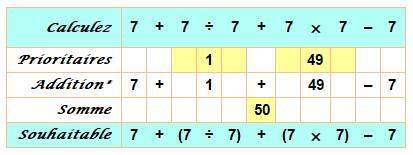
Ce calcul
est proposé en quizz sur Internet pour tester vos connaissances de CM2. Ce dont il
faut se rappeler: les multiplications et divisions sont prioritaires: on les
calcule en premier. Pour
éviter les confusions (voire les pièges), il est conseillé de mettre les
parenthèses comme indiqué en dernière ligne du tableau. |
Quizz
*
Addition au sens addition algébrique (qui peut
comporter des signes moins). Écriture plus formelle
|
|
|
|
|||
|
Priorité des
opérations:
On aurait pu
mettre des parenthèses: (2x3) + 2 = 6 +
2 = 8. On convient que,
sans parenthèse, on effectue la multiplication en premier: 2x3 + 2 = 6 + 2
= 8 et non pas 2x3 +
2 qui donnerait 2 x 5 = 10. |
Exemples 2x3 +
10/2 + 7 + 8 – 9 = 6 +
5 + 7 + 8 – 9 = 17 7,2 x
4 – 2,5 x 1,3 + 10,2 = 28,8 –
3,25 + 10,2 = 35, 75 |
||
|
Priorités aux parenthèses s'il y en a. Priorité aux parenthèses les
plus profondes. |
(2+3)
x 4 + (10+2) / 6 + 17 =
(5) x 4 + (12)
/ 6 + 17 = 20
+ 2 + 17 = 39 ((2x3 + 4) x 5 + 6) x (18/2-4) =
(( 6
+ 4) x 5 + 6) x ( 9 -4) =
( 10 x 5 + 6) x ( 9
-4) =
( 50 + 6) x ( 9
-4) =
( 56) x ( 5) = 280 |
||
|
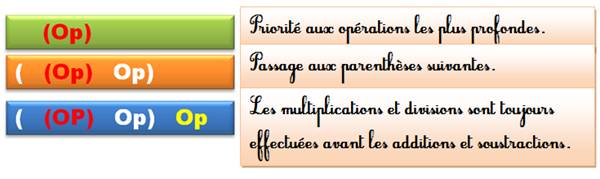
En résumé (Op veut dire
opérations) |
|
||
Bilan
|
L'usage des
parenthèses n'est qu'une convention de
notation. Elles représentent un
"paquet" de calculs à effectuer en premier avant de libérer le
résultat pour des calculs ultérieurs. Il faut prendre le
temps de bien comprendre cet usage. Il
n'est pas rare de retrouver des élèves en seconde qui ont
encore des difficultés avec les parenthèses (sans trop s'en rendre compte). |
|
|
|||
|
16 est la somme
de 12 plus 4. 10 est la différence entre 12 et 2. 24 est le produit
de 12 par 2. 2 est le quotient de 12 divisé par 6 |
12 + 4 = 16 12 – 2 = 10 12 x 2 = 24 12 / 2 = 6 ou |
|
|
|
A est
égal au produit de 2 par la somme de 3 et 4. B est
égal au quotient de 20 par la différence entre 7 et 2. C est le
quotient par 7 d'un produit de deux sommes, l'une égale à 2 plus 3 et l'autre
égale à 4 plus 5. |
A = 2 x (3 + 4) = 2 x 7 = 14 B = 20 / (7 – 2) = 20 / 5 = 4 C = (2 + 3) x (4 + 5) / 7 =
5 x 9 / 7 = 45/7 |
||
Voir Ordre
des opérations et besoin de parenthèses
|
|
||
|
Méthode classique (vue
ci-dessus): Méthode distributive: |
2 x (3 + 5) = 2 x 8 = 16 2 x (3 + 5) = 2 x 3 + 2 x 5 = 6 + 10 = 16 a x (c + d) = a x c + a x d |
|
|
Illustration: 2 paquets de bonbons identiques, chacun
contenant 3 bonbons verts et 5 rouges.
|
||
|
Résumé avec des lettres remplaçant les nombres On dit que la multiplication
est distributive par rapport à l'addition. |
a x (c + d) =
a x c + a x d |
|
|
À l'envers et de diverses
manières … Inverser les
nombres dans un produit (simple ou avec parenthèses) ne change pas la valeur
du produit. Faire des paquets (mettre
entre parenthèses) s'appelle factoriser ou
mettre en facteurs commun. Utiliser des lettres à la
place des nombres s'appelle faire de l'algèbre. |
Exemples numériques 4 x 5 + 4 x 7 = 4 x (5 + 7) 5 x 4 + 7 x 4 = (5 + 7) x 4
= 4 x (5 + 7) Dans le produit 4 x 5, les facteurs
sont 4 et 5. Dans le produit 4 x 7, les facteurs sont 4 et 7. Le nombre 4 est un facteur commun à ces deux produits; on peut
factoriser, c'est-à-dire, faire un paquet avec (5 + 7) et le compter 4 fois. Algèbre: on peut écrire de diverses façons a x c + a x d = a x (c + d) = c x a + d x a = (c + d) x
a = a x d + c x a = a (d + c)
= (c + d) x a |
|
|
Problème Le chariot-élévateur dépose
10 cageots de 25 poires, puis 10 cageots de 32 pommes dans la chambre-froide. En utilisant la factorisation,
calculez la quantité de fruits. Autrement-dit,
le conducteur aurait pu rassembler pommes et poires dans des cageots plus
grands. |
J'explique 10 cageots de 25 poires + 10 cageots de 32 pommes = 10 cageots de (25 + 32)
fruits = 10 cageots de 57 fruits =
570 fruits Je calcule 10 x (25 + 32) = 10 x 57 = 570 |
|
|
|
||
|
Parfois, on souhaite donner
une relation sans mentionner les nombres. Une voiture qui va à une
vitesse de 100 km/h parcourra 200 km
en 2 heures ou 500 km en 5 heures ou, d'une manière générale: L = V x T L: longueur
parcourue à la vitesse V en une
durée égale à T. En remplaçant des nombres
par des lettres, nous passons de l'arithmétique à l'algèbre. Un des problèmes que se pose
l'algèbre consiste à calculer la valeur de certaines lettres qui sont alors
baptisée x ou y ou z. |
Exemple d'une expression typique: a x b + c + 3 x a + 5 x c Pour éviter le x
qui est aussi une lettre, on le sous-entend: ab + c + 3a + 5c Si une confusion
est possible, on met un point entre les lettres: a.b + c + 3a + 5c Pour plus de clarté,
on utilise l'ordre alphabétique 3a + ab + c + 5c S'il y a lieu,
on regroupe les termes identiques 3a + ab + 6c Nous connaissons
la factorisation; Appliquons! a (3 + b) + 6c |
|
|
Une équation est une
égalité. Le but est de trouver un nombre remplaçant une lettre (x) qui
satisfait l'égalité, la solution. |
3x = 6
solution x = 2 3x + 2x = 10 solution
5x = 10 et x = 2 3x = 10 – 2x solution
x = 2 car 6 = 10 – 4 |
|
|
Je vérifie la valeur si je la
connais! Mais comment la trouver? Par curiosité voici un exemple, mais cela
sera étudié plus tard. |
3x = 10 – 2x J'ajoute la même
quantité de chaque côté sans changer l'égalité (pensons aux plateaux d'une
balance). 3x +
2x = 10 – 2x + 2x Je calcule: 5x = 10 solution x = 2 |
|
|
|
||
|
Pour se mettre en rang par 2
parfaitement, il faut que la quantité d'élèves soit un nombre qui se termine
par 0, 2, 4, 6 ou 8. La somme de deux
nombres consécutifs, comme 2 + 3 = 5, n'est jamais divisible par 2; cette
somme est toujours impaire. Le produit de
deux nombres consécutifs, comme 2 x 3 = 6, est toujours divisible par 2: ce
produit est pair. |
2, 4, 6, 8, 10, 12, 14, 16,
18, 20, … élèves Ces nombres sont des multiples de 2, ce sont des nombres pairs. |
|
|
Pour se mettre en rang par 5
parfaitement, il faut que la quantité d'élèves soit un nombre qui se termine
par 0 ou 5. |
5, 10, 15, 20, 25, … élèves Ces nombres sont des
multiples de 5. 5 est un diviseur de ces nombres |
|
|
Pour se mettre en rang par
10 parfaitement, il faut que la quantité d'élèves soit un nombre qui se
termine par 0. Un nombre
divisible par 10 est aussi divisible par 2 et par 5 car 10 = 2 x 5. |
10, 20, 30, 40, 50, … élèves Ces nombres sont des
multiples de 10. 5 est un diviseur de ces nombres |
|
|
Pour se mettre en rang par 4
parfaitement, il faut que la moitié de la quantité d'élèves soit un nombre
pair. Attention, un
nombre qui se termine par 4 n'est pas toujours divisible par 4. |
4, 8, 12, 16, 20, 24, 28, …
élèves la moitié: 2, 4, 6,
8, 10, 12, 14 … |
|
|
Pour se mettre en rang par 3
parfaitement, il faut que la somme des chiffres du nombre soit divisible par
3. |
3, 6, 9, 12, 15, 18, 21, 24
… élèves Exemple: 24 |
|
|
Pour se mettre en rang par 9
parfaitement, il faut que la somme des chiffres du nombre soit divisible par
9. Un nombre
divisible par 9 est aussi divisible par 3. |
9, 18, 27, 36, 45, 54, 63 …
élèves Exemple: 63 |
|
Voir Divisibilité
– Débutants / Accès à tous ces
nombres: DicoNombre
|
|
||
|
Diviser une tarte en 8,
c'est la fractionner en 8 parts. En prendre une part, c'est prendre un
huitième de tarte. Dénominateur pour dénommer la quantité de
parts; Numérateur pour indiquer le nombre da parts que
l'on prend. |
Une fraction est le quotient
de deux nombres entiers; numérateur en haut et dénominateur
en bas.
|
|
|
Couper la tarte en part deux fois plus petites (en 16) et en prendre deux fois plus (2parts) ne change pas la portion. |
La valeur de la fraction ne
change pas si on multiplie le numérateur et le dénominateur par le même
nombre (sauf par 0).
|
|
|
Cette règle, appliquée à la multiplication
comme à la division, permet de retrouver des parts entières. |
|
|
|
Elle permet également de
calculer des pourcentages en trouvant un nombre qui multiplié par le dénominateur
donne 100. |
|
|
|
Problème Cette société exige 2
représentants pour 50 personnes. Quel est le pourcentage? Cette société compte 450 personnes.
Combien faut-il de représentants? |
Pourcentage
Représentants
La réponse est: 18 représentants. |
|
|
|
||
|
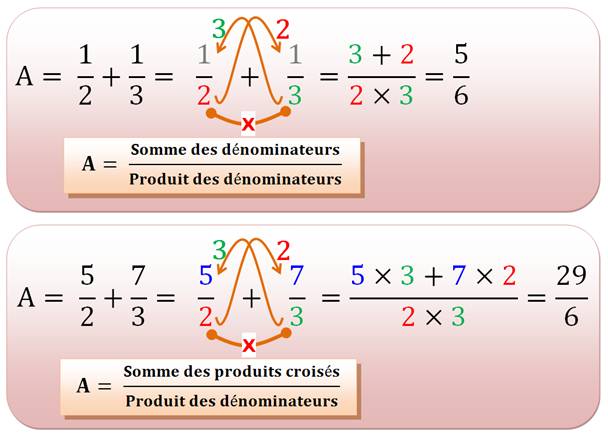
Pour ajouter des fractions,
il faut ajouter des parts de même taille: des quarts, des huitièmes ou
autres. Si les parts ne sont pas
égales, on découpe en parts plus fines, telles que les parts soient égales
pour chacune des fractions. |
Même
dénominateur
Dénominateurs
différents
|
|
|
Dans tous les cas, on
simplifie les fractions. |
|
|
|
Un nombre entier est une
fraction dont le dénominateur est égal à 1. |
|
|
|
Problème Le quart des élèves étudient
l'anglais. Un huitième l'allemand. Tous les autres étudient l'espagnol. Ils sont
combien en pourcentage? |
|
|
|
En résumé
Idem pour la soustraction en
remplaçant somme par différence. |
||
|
|
||
|
La tarte est découpée en
quarts Gourmand, je prends une part
trois fois de suite. J'ai englouti trois quarts de tarte. Mon copain prend la moitié
d'un part. Le pauvre ça ne lui fait qu'un huitième de tarte. |
|
|
|
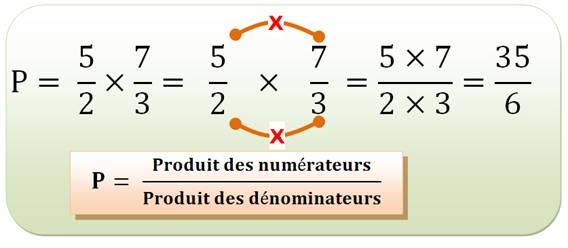
D'une manière générale: On multiplie les numérateurs entre eux et
les dénominateurs entre eux. |
|
|
|
On simplifie dès que
possible: |
|
|
|
En résumé
La division sera étudiée
plus tard (Pour les impatients: diviser par ½ reviens à multiplier par 2). |
||
|
|
|||
|
Je dispose de 10 euros,
c'est 10€ dans ma bourse. J'ai emprunté 10 euros,
alors non seulement j'ai 0€ dans ma bourse, mais dès que j'en aurai gagné 10,
il faudra que je les donne. C'est comme si j'avais actuellement j'avais:
-10€. Je remarque déjà
que 10€ gagnés efface ma dette de 10€. –10€ + 10€ = 0€ Si j'avais gagné
12€, il me resterait même 2€. –10€ + 12€ = 2€ |
La température peut être
positive ou négative s'il gèle. Une entreprise peut avoir
des bénéfices (+) ou des pertes (-). L'altitude des montagnes est
positive, celle des océans est négative. |
||
|
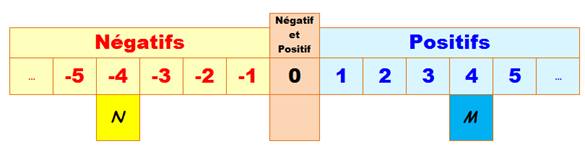
La droite des nombres entiers relatifs
La position de M est appelée
son abscisse, elle vaut +4 (sans confusion
on note 4). L'abscisse de N est –4. Les
deux points M et N sont à égale distance du 0; ils sont symétriques. On dit que les deux nombres 4 et –4
sont des nombres opposés. |
|||
|
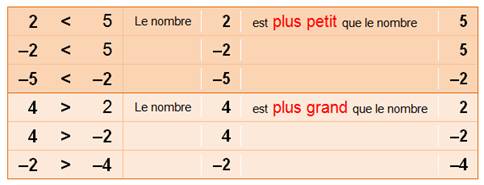
Un nombre plus à droite
qu'un autre est plus grand. Un nombre plus à gauche
qu'un autre est plus petit. |
Exemples
|
||
|
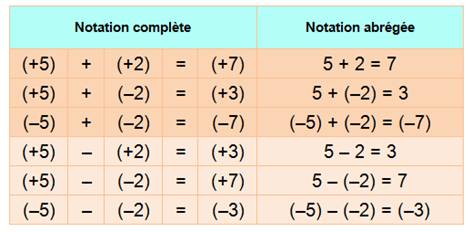
Additions et soustractions
des nombres relatifs. Pour faire ces opérations,
je visualise l'opération sur la droite des nombres. La seule
difficulté: soustraire un nombre négatif, notion qui sera vue plus tard. |
|
||
|
En résumé
|
|||
Voir Nombres
relatifs / Soustraction
/ Plus par plus
|
Somme, différence,
produit et quotient; Diviseur,
divisibilité, multiple; Algèbre, équation
et sa solution; Facteur,
factoriser: Distributivité; Numérateur,
dénominateur; Droite des
nombres, abscisse; et Nombre négatif,
relatif, opposé, symétrique. |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()