NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 15/01/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Puissances
Débutants Logarithmes	Triplets de Pythagore				Glossaire Puissances
Rubrique PARTITION INDEX PUISSANCES	Introduction	Propriétés	Cercle	Historique
	Primitif	Génération	Matrice	Spéciaux
	Illustration	Triangles	Briques	Calculs
	Avec un carré			TABLES
	Sommaire de cette page >>> Triplets doublement carré >>> Jumeaux >>> Fibonacci >>> Curiosités >>> La famille du triplet 5, 12, 13

TRIPLETS de PYTHAGORE

Spéciaux

Avec des nombres particuliers.

Triplets doublement carré
a + b = c² et a² + b² = d² Triplet de Pythagore dont la somme des deux termes est aussi un carré. Le plus petit cas et, en plus, double motif.	Plus petit exemple 9 + 40 = 7² = 49 9² + 40² = 41² = 1 681 Mise en évidence du double motif pour 49 49 = 7² = 9 + 40 et 9² + 40² = 41² = 1 681 49 = 7² = 21 + 28 et 21² + 28² = 35² = 1 225
Liste des triplets dont la somme des deux premiers termes est aussi un carré Table pour a et b jusqu'à 1000 Notez que la présentation en double motif est fréquente: 49, 196, 441, 289, … Par ailleurs, inutile de chercher le même type de motif avec des cubes du fait du théorème de Fermat-Wiles: a^3 + b^3 = c^3 n'existe pas en nombres entiers. Avec des nombres négatifs, par exemple: (-3) + 4 = 1² et (-3)² + 4² = 5² Avec trois termes: de très nombreuses présentations. a + b + c = d² et a² + b² + c² = e² 1 + 6 + 18 = 5² et 1² + 6² + 18² = 19² = 361 1 + 12 + 12 = 5² et 1² + 12² + 12² = 17² = 289 … 20 + 40 + 40 = 10² et 20² + 40² + 40² = 60² = 3 600 … 48 + 64 + 84 = 14² et 48² + 64² + 84² = 116² = 13 456 49 + 50 + 70 = 169 = 13² et 49² + 50² + 70² = 99² = 9 801 a + b + c = d^3et a^3 + b^3 + c^3 = e^3 54 + 72 + 90 = 6^3 = 216 et 54^3 + 72^3 + 90^3 = 108^3 = 1 259 712 81 + 696 + 951 = 12^3 = 1 728 et 81^3 + 696^3 + 951^3 = 1 062^3 = 1 197 770 328

Voir Somme de carrés de nombres consécutifs

JUMEAUX

Triplet jumeau

Un triplet est dit jumeau si l'hypoténuse dépasse d'une unité l'un des côtés

(a, b, b + 1)

Un triplet jumeau implique qu'un nombre au carré est la différence de deux nombres consécutifs au carré

a² = (b+1)² - b²

Les triplets suivants avec a impair sont jumeaux (connu de Pythagore)

( a, 1/2(a² - 1), 1/2(a² + 1) )

ou en multipliant par 2

(2b, b² - 1, b² + 1)

Voir Formule équivalente à partir d'un nombre n unique

Exemples

a	3	5	7	9	11	13	15	17	19	21	23	25
1/2(a²-1)	4	12	24	40	60	84	112	144	180	220	264	312
1/2(a²+1)	5	13	25	41	61	85	113	145	181	221	265	313

Suite

27, 364, 365
29, 420, 421
31, 480, 481
33, 544, 545
35, 612, 613
37, 684, 685
39, 760, 761
41, 840, 841
43, 924, 925

45, 1012, 1013
47, 1104, 1105
49, 1200, 1201
51, 1300, 1301
53, 1404, 1405
55, 1512, 1513
57, 1624, 1625
59, 1740, 1741

61, 1860, 1861
63, 1984, 1985
65, 2112, 2113
67, 2244, 2245
69, 2380, 2381
71, 2520, 2521
73, 2664, 2665
75, 2812, 2813
77, 2964, 2965
79, 3120, 3121

81, 3280, 3281
83, 3444, 3445
85, 3612, 3613
87, 3784, 3785
89, 3960, 3961
91, 4140, 4141
93, 4324, 4325
95, 4512, 4513
97, 4704, 4705
99, 4900, 4901
101, 5100, 5101

Anglais: Twin triple

FIBONACCI

Triplets de Fibonacci

Il est possible de format un triplet de Pythagore impliquant des nombres de Fibonacci de la manière suivante

( F_n . F_n+3 , 2 F_n+1 . F_n+2 , F_n+1² + F_n+2² )

Démontré par Horodam(1961) et Dujella (1987)

Exemples

n	1	2	3	4	5	6	7	8	9	10
Fn	1	1	2	3	5	8	13	21	34	55
Fn . Fn+3	3	5	16	39	105	272	715	1 869	4 896	12 815
2 Fn+1 . Fn+2	4	12	30	80	208	546	1 428	3 740	9 790	25 632
Fn+1² + Fn+2²	5	13	34	89	233	610	1 597	4 181	10 946	28 657

CURIOSITÉS
Voir Triangles

La famille du triplet 5, 12, 13		haut
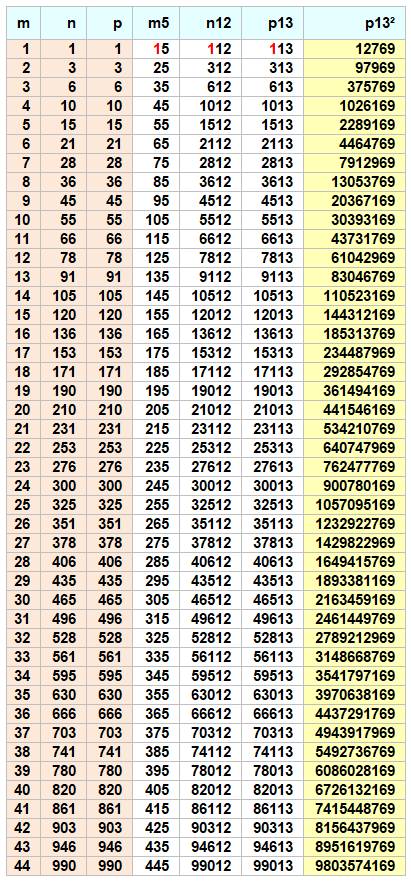
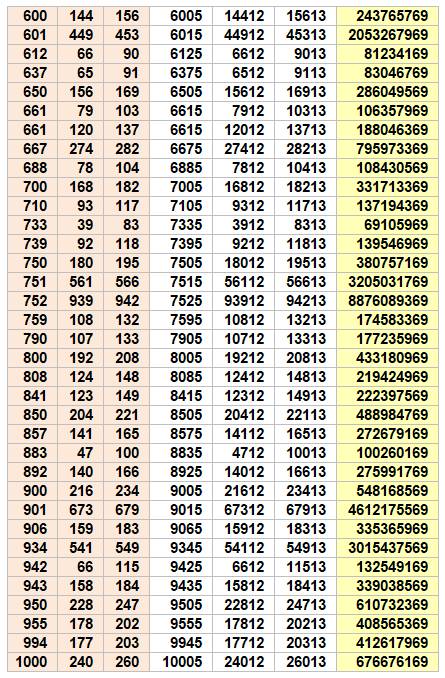
Chaque terme du triplet est complété à gauche par un nombre, respectivement, m, n et p. Jusqu'à 10 000, il y a une descendance de 115 triplets. Le seul avec m = n = p est le premier listé: (15, 112, 113).

Suite	Triplets - illustration
Voir	Addition - Glossaire Années Pythagore Décade de Pythagore Pythagore - Biographie
Site	Pythagorean Triple de Eric Weisstein
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/TripSpec.htm