|
|||||||||||||||||||||||||||||||||||
![]()
|
DIVISIBILITÉ par 37 Critère de divisibilité par 37
(valable aussi pour 27):
Notez que: 37 x 3 = 111
et 37 x 27 = 999 = 1000
– 1. |
Voir Divisibilité par 37
(terminale)
|
|
||
|
Procédé expliqué sur un exemple.
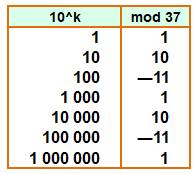
Explication Les restes de la division par 37 des puissances
de 10 forment un cycle {1, 10, 26} que l'on peut aussi écrire {1, 10, -11}
avec 26 – 37 = –11 Alors un nombre comme: Le nombre 2368 est divisible par 37 (2368 = 37 x
64). |
Exemple de calcul de divisibilité
par 37
La différence des deux sommes est nulle, le nombre est divisible par 37: Restes des puissances de 10
divisées par 37
|
|
Voir Brève
798
|
|
||
|
Nombres divisibles par
37 (ou multiples de 37): 1 chiffre: aucun. 2 chiffres: 37 et 74 3 chiffres: 111, 148, 185 … 222 … 333 … 999. Notez que: 11 multiples
à trois chiffres sur 25 sont facilement reconnaissables. |
Comment reconnaitre si un nombre à trois chiffres est divisible par
7? Comme tous les repdigits (111, 222, 333 …) sont divisibles par 37, il suffit de
calculer la "distance" à un de ces nombres. Exemples: 456 divisible par 37? 456 – 444 = 12 481 divisible par 37? 481 – 444 = 37 |
|
|
Les nombres repdigits de 3k
chiffres sont divisibles par 37. Les nombres dont les blocs de trois sont des repdigits sont divisibles
par 37. Attention: Ne pas en
déduire qu'un nombre est divisible par 37 si ses blocs de trois chiffres le
sont. |
333 333 333 = 333 . 106 + 333 . 103 + 333 = 9 . 37 .106 + 9 . 37 .103 + 9 . 37 = 9 . 37 (106 + 103
+ 1) 333 666 777 = 333 . 106 + 666 . 103 + 777 = 9 . 37 .106 + 18 . 37 .103 + 21 . 37 = 37 (9 .106 + 18.103
+ 21) |
|
|
|
||
|
|
||
|
|
|||
|
Si un nombre de trois chiffres est divisible par 37, toutes ses
permutations circulaires le sont. Attention: Ne pas en
déduire Que cela est vrai pour tous les blocs de trois chiffres dans un
nombre; ni pour les trois derniers chiffres d'un nombre de plus de trois
chiffres. |
Démonstration
Idem pour l'autre configuration en 100u + 10c + d Exemple 148, 481 et 814 sont divisibles par 37. |
||
|
Les cas de divisibilité par
permutations circulaires (PC) sont nombreux: Ci-contre, l'exemple montre
les six permutations circulaires; elles sont toutes divisibles par 37. Les permutations circulaires
sur les blocs de trois chiffres ne sont
divisibles par 36 que pour les trois permutations synchronisée. Soit un nombre de 3k chiffres. Toutes les PC sur l'ensemble des
chiffres sont divisibles par 37, ainsi que toutes les PC synchronisées sur
chaque bloc de 3 chiffres. Prudence si le dernier
bloc de gauche ne comporte pas trois chiffres, ajouter les 0 nécessaires! |
Exemple
|
||
|
|
||
|
Règle On se ramène à un nombre de
trois chiffres au plus en ajoutant tous les blocs de trois chiffres du
nombre. |
Exemples 123 456 789 divisible par 37 ? 123 + 456 + 789 = 1 368 1 368 = 1 + 368 = 369 369 – 333 = 36 De justesse! Manque une unité. Alors 123 456 790 est sûrement divisible par 37. 123 + 456 + 790 = 1 369 1 + 369 = 370 |
|
|
Pourquoi cela marche? |
Cela tient au fait que 999, proche de 1000 est
divisible par 37 |
|
|
Séparons le nombre N en blocs
de trois chiffres et indiquons que ce nombre est divisible par 37. |
Voir Modulo Exemple 45 678 979 = 45 x 106 + 678 x 103 + 979 |
|
|
Exploitons le fait que les
nombre 999, 999999 … sont des nombres divisibles par 37. De même que tous leurs
multiples. Note: comme 999 est aussi divisible par 27, cette démonstration est valable
pour 27. |
Etc. |
|
|
Retranchons de tels nombres
de chaque côté de l'égalité. Limitons nous à 106 pour faciliter l'écriture. La méthode
s'applique à aux puissances 3 k suivantes |
|
|
|
En ne conservant que la
partie de droite et en effectuant les soustractions. Introduisons également
le fait que cela est vrai pour les blocs de trois de puissances supérieures. |
|
|
|
Miracle! Nous avons la somme
des blocs de trois! |
Il suffit de tester la
somme des blocs de trois chiffres. |
|
|
Demander à choisir un
nombre de trois chiffres. |
321 |
|
Mentalement calculer
le complément à 555 ou à 999. |
234 |
|
Prétendez que vous
avez un nombre divisible par 37 incluant le sien. |
234 321 ou 321 234 |
Voir Magie
|
|
||
|
|
Exemples 1 369 divisible par 37 ? 136 – 9 x 11 = 37 1 369 138269 divisible par 37 ? 13826 – 9 x 11 = 13 727 13 72 – 7 x 11 = 1 295 129 – 5 x 11 = 74 138 269 93 092 9309 – 22 = 9 287 928 – 77 = 851 85 – 11 = 74 |
|
|
Programmation sur tableur Voici un exemple avec un
nombre de 10 chiffres non répétés, programmé
sur tableur. Notez que dans ce cas N est un pannumérique
(tous les chiffres, une fois). Pour chaque ligne N est égal
à N' de la ligne précédente. |
|
|
|
|
||
|
Voir le cas des pannumériques divisibles par 11 |
Quantité de nombre pannumérique à 10 chiffres Premier chiffres: de 1
à 9 Pour les neuf autres:
de 0 à 10 Soit: 9 x 9! = 3 265 920. Quantité de tels nombres divisible par 37 Dénombrement par
programme: 85 104 Ces permutations sont divisibles par 37
Etc. Au total 63 tels
nombres permutés. |
|
Quantité de nombres à "Qté" de
chiffres distincts, divisibles par 37

English corner
|
Subtract eleven times the last digit
from the remaining leading truncated number. If the result is divisible by 37,
then so was the first number. Apply this rule over and over again as
necessary. |
![]()
|
Avec 37 |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divisi37.htm
|
![]()