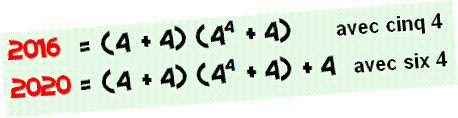|
Édition du: 20/08/2021 |
|
INDEX |
Nombres = opérations sur chiffres |
||||
|
Quatre 4 (avec
quatre 4 de 0 à 70) |
|||||
|
Quatre 4 (avec
quatre 4 de 70 à 200) |
|||||
|
Quatre 4 –
Difficultés – Curiosités |
|||||
![]()
|
Jeu des QUATRE 4 – de 70 à 200 Comment
atteindre le nombre n avec des opérations combinant quatre fois le même
chiffre, en l'occurrence le 4. Au-delà
de 70, les solutions deviennent difficiles à trouver. Elles requièrent
souvent des opérations avancées. Le nombre 113
est le plus petit à résister. On connait des solutions jusqu'à 40 000 avec
quelques manques. |
||
|
|
Sommaire de cette page >>> 4 quatre > 70 >>> Cas
difficiles et impossibles >>> Solutions >>> La solution
universelle en quatre 4 |
Débutants Glossaire |
Années avec chiffres 4
|
Solutions
avec quatre 4
|
Voir Année 2016 / Année 2020 / Nombre 2019
/ Nombre
2020
Voir Opérations utilisées pour résoudre les cas
difficiles





Voir Autres solutions, notamment pour 113


Voir Solution pour 157 avec fonction gamma et autres
solutions

Voir Solution pour tous les manquants avec introduction de symboles spéciaux
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()