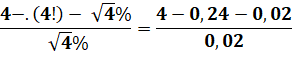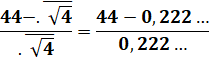|
Édition du: 23/12/2020 |
|
INDEX |
Nombres = opérations sur chiffres |
||||
|
Quatre 4 (avec
quatre 4 de 0 à 70) |
|||||
|
Quatre 4 (avec
quatre 4 de 70 à 200) |
|||||
|
Quatre 4 –
Difficultés – Curiosités |
|||||
![]()
|
Jeu des QUATRE 4 Résolution des difficultés –
Curiosités Comment
atteindre le nombre n avec des opérations combinant quatre fois le même
chiffre, en l'occurrence le 4. Liste des
possibilités pour tous les nombres de 0 à 70. Liste des
opérations, fonctions et symbole utilisés pour résoudre les cas
pathologiques. >>> On notera
la solution universelle permettant d'atteindre tous les nombres jusqu'à
l'infini. >>> |
||
|
|
Sommaire de cette page >>>
Symboles, opérations et fonctions >>> Cas particuliers >>> Analyse des cas
difficiles >>> La solution
universelle en quatre 4 >>> Belles formes et
curiosités |
Débutants Glossaire |
Anglais: 4444 (Four Fours) / Four 4's puzzle
![]()
|
Nous relevons cinq cas difficiles pour
arriver à 100 et d'autres ensuite. Aujourd'hui aucune solution n'a été
découverte avec la liste des symboles autorisés pour
113. Il semble que pour trouver une
solution, il faille recourir à d'autres symboles mathématiques. Voici quelques idées. Celles en
jaune foncé me semble les plus acceptables. Peter Karsanow donne des règles
précises au jeu. Sa limite est 183. Il utilise le symbole ² du carré.
David Wheeler a atteint 40 000 avec quelques
manques. |
|||
|
.4 = 0,4 = 2/5 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
!4 |
! 4 = 9 |
||
|
4!! |
|
||
|
!!4 |
|
||
|
4# |
|
||
|
.04 |
|
.04 vaut 0,04 |
|
.(f) |
|
. |
|
i 4 = 1 |
|
|
|
x² |
|
|
|
|
|
|
|
Ck |
k est
l'indice de répétition du chiffre |
|
|
|
|
|
|
% |
|
(4+44)%
+ .4 = 3 |
|
ENT[x] |
Permet d'arrondir
vers le bas. |
ENT [
|
|
Fonctions |
Voir
Solution
universelle >>> |
log4(44)
= 4 |
|
|
|
|
|
4' |
4' = 1/5 = 0,25 |
|
|
|
|
|
99 = |
|
||
|
100 = |
|
||
|
500 = |
|
Voir Explications |
|
|
5 000 = |
|
||
|
10 000 = |
|
||
|
40 000 = |
|
||
|
17 = |
|
|
|
37 = |
|
|
|
69 = |
|
|
|
73 = |
|
|
|
77 = |
|
|
|
81 = |
|
|
|
87 = |
|
|
|
93 = |
|
|
|
99 = |
Voir
Autres explications |
|
|
103 = |
|
|
113 = |
Plus
petit nombre sans solution simple. Note:
4' = 1/4 |
|
117 = |
|
|
145 = |
|
|
|
|
|
163 = |
|
|
164 = |
Voir Nombre
164,8… |
|
166 = |
|
|
167 = |
|
|
171 = |
|
|
173 = |
|
|
185 = |
|
|
187 = |
|
|
191 = |
|
|
193 = |
|
|
197 = |
|
|
199 = |
|
|
Tout
nombre rationnel peut être atteint par les logarithmes. Exemple
Calcul
machine
Principe Autant de signes racine
que le nombre à atteindre. Ici, 3 en haut et 4
en bas.
Plus
simplement
Tout repose sur ces identités pour n > 1:
Voir Logarithmes
Détail
du calcul pour l'exemple
Voir Calculs avec les logarithmes / Tables de log |
|
|
Solution
universelle avec la trigonométrie 5
= sec(atan (sec(atan (sec(atan (sec(atan (sec(atan (sec(atan (sec(atan
(sec(atan (sec(atan (4)))))))))))))))))) Pour
obtenir n, il faut n² – 16 fois sec(atan), soit 9 pour avoir 5. |
|
|
Forme complexe
avec des 4: –1024 = (4 + 4i)4 = (4 – 4i)4 Développement
de la puissance 4:
Avec a =
i
|
Voir Pépites
/ Identités
remarquables
Original! Fraction avec deux 4
|
|
Voir Comment faire 99 avec quatre 4 / Nombre
0,125
Solution
universelle (atteint tous les nombres jusqu'à l'infini)
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()