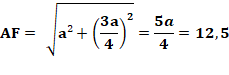NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/12/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométrie ÉLÉMENTS de base
Débutants Géométrie Junior Découverte des quadrilatères	Généralités			Glossaire Géométrie
INDEX Carré Géométrie	Quadrilatère	Carré – Introduction	Construction
	Aire	Carré – Propriétés	Passage du bassin
		Sommaire de cette page >>> Sécantes orthogonales >>> Médianes et semi-médianes >>> Diagonale brisée >>> Rotation – Bon à savoir >>> Deux carrés >>> Équation du carré oblique

Carrés – Propriétés

Devinette

Combien de possibilités de couper ce carré en deux parties égales en suivant les lignes du quadrillage ?

Solution

Sécantes orthogonales
Théorème Dans un carré deux sécantes orthogonales découpent des segments de même longueur. Les segments bleus ont même longueur quelle que soit la position du point de croisement. Démonstration Dans les triangles rectangles semblables avec l'angle alpha: Or, a + b = c + d => x + y = v + w Voir Construction du carré passant par quatre points

Médianes et semi-médianes
Carré ABCD, E milieu de BC et F et G milieux de BE et EC. Quelle est la longueur de la médiane AE et celles des semi- médianes AG et AF ? Diagonale AC avec AB = a = 10 Longueurs des segments Angles

Voir Médianes du triangle équilatéral / Diagonales des polygones

Diagonale brisée
Énigme On connait les dimensions de cette diagonale brisée à angles droits. Trouver la longueur du côté du carré. Solution Tracer la diagonale (verte) et translater deux segments de sorte que l'on retrouve un triangle rectangle. Avec Pythagore: D² = 21² + 3² = 450 D = 15 Encore Pythagore pour le côté: C² + C² = D² = 2 C²	Carré avec diagonale brisée Détail pour solution

ROTATION – Bon à savoir!
La longueur d'un segment est conservée suite à une rotation. Cette propriété anodine va nous servir Même si la rotation n'apparaît pas toujours au premier coup d'œil.

Deux carrés
Deux carrés avec un sommet commun A. On dessine les deux segments indiqués en rouge. On va démontrer que ces deux segments sont égaux (de même mesure) et disposés à angle droit.
Rotation de centre A d'un angle de 90 ° B devient D et b devient d
C'est vrai pour les segments ayant ces extrémités		Bb devient Dd Bd et Dd ont même longueur
C'est une rotation de 90°		Bb est perpendiculaire à Dd
Exemples de cas extrêmes

Équation du carré oblique
Question Quelle est l'aire de la région limitée par cette équation ? Réponse La région est délimitée par ces quatre droites: Le graphe montre que cette région est un carré orienté à 45° dont le côté vaut racine de 2.

Devinette – Solution

Les six façons de couper le carré en deux parties égales

(hors symétries et rotations)

Retour / Autres énigmes

Suite	Carré – Suite Aire du carré Carré rigide Carré dans le cube Carré découpé en 5 Construction du carré passant par quatre points Doubler le carré Découverte des quadrilatères – Juniors
Angles	90° 180° 360° Sommes des angles
Voir	4 Couleurs Carré dans le triangle Carré rigide Carré et rectangle à trou Géométrie – Index Jeux – Index Nombres Carrés Pavage du carré Quadrature du cercle Quadrilatère Quantité de carrés avec des allumettes Tangram
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/CarrProp.htm