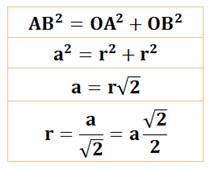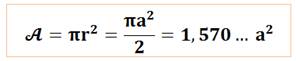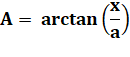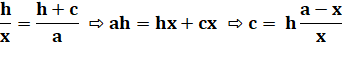|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
AIRE du CARRÉ & variations autour des aires L'aire du carré est simple à calculer. Mais, sauriez-vous construire trois carrés
concentriques tels que les couronnes découpées soient de même aire que le
carré central? Et, calculer l'aire d'un
carré construit en oblique dans un carré plus grand? |
|
|
||
|
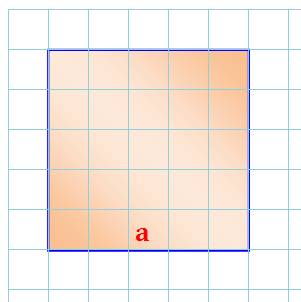
Sur ce carré pavé de dalles
carrées, la quantité de dalles est égale à 25. En fait, 5 rangées de 5
dalles, soit 5 x 5 = 25 dalles. L'aire du carré es égale au carré de la
mesure de son côté.
Ne pas confondre avec le
périmètre (le tour du carré) qui vaut 4a. |
Aire
de ce carré: 5 x 5 = 25 Son
périmètre: 4 x 5 = 20 |
|
|
Le triangle AOB est isocèle: OA = OB = r,
rayon, du cercle circonscrit. Il est aussi rectangle (l'angle AOB est droit). Le théorème de Pythagore s'écrit:
Notez que: si r = 1, alors a = Aire du cercle circonscrit:
Il peut paraître surprenant
que l'aire du cercle soit
plus de 1,5 fois celle du carré. Pour mieux apprécier la surface occupée par
les quatre segments (bleus), retournons-les dans le carré. Cette forme rose occupe une aire de:
|
Sur
la figure, a = AB = 6 unités et OH = 3 unités.
L'aire de la forme rose vaut moins
de la moitié de celle du carré. |
|
|
|
||
|
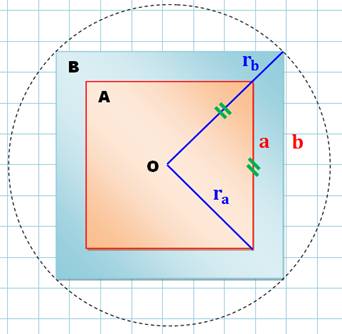
Problème Deux carrés A et B,
concentriques de côté a et b. Nous souhaitons que la
couronne découpée par le carré A dans le carré B soit de même aire que le
carré central. Calculs
|
Aire bleue
= aire rose La couronne bleue a la même aire
que le carré rose central si le rayon de son cercle circonscrit (la
demi-diagonale du carré bleu) est égale au côté du carré rose. |
|
|
Vérification de la formule (exercice) L'épaisseur de la couronne
est égale à L'aire de la couronne vaut
quatre fois les carrés des angles et quatre fois les rectangles latéraux. L'aire de la couronne est bien égale à 1. Construction Dessin à la règle et au
compas: après avoir dessiné le carré, ouvrir le compas à la taille du côté
du carré (a) et dessiner un cercle de centre O; prolonger les diagonales du
carré; les intersections avec le cercle sont les sommets du carré recherché. |
Calcul de l'aire de la couronne
|
|
|
avec couronnes de même aire que le carré central |
|
|
|
Vous pouvez itérer
(recommencer sans fin) cette construction avec le nouveau carré (bleu), pour
former une couronne de même aire.
Calcul:
Segment AB en vert
|
Dessin de cette figure à la règle et au compas
|
|
Voir Construction géométrique des nombres
|
|
||
|
CAS 1) – Coordonnées de sommets Un plus petit carré (jaune)
est dessiné dans un grand carré (bleu de côté a) tel que chacun de ses
sommets est à égale distance des sommets du grand, définie par la valeur de x
et y. Calcul via l'extérieur Aire de la couronne bleue B = 4 (C + R + T) = 4 (x² + x(a – 2x) + ½ (y – x) (a – x – y) = 2x (a – x) + 2y (a – y) Attention à prendre y – x, valeur positive, ou la valeur absolue de la
différence. Aire du carré jaune J = a² – 2x (a –
x) – 2y (a – y) Vérification J = 100 – 2.2.8 – 2.3.7 = 100 – 32 – 42 = 26 |
Calcul via l'intérieur Aire du carré jaune J = (a – 2y)² – 2 (y – x) (a – x – y) = … = a² – 2x
(a – x) – 2y (a – y) Le développement
des calculs est à peu près le même. |
|
|
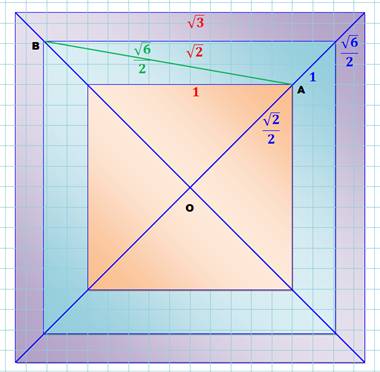
CAS 2) – Les quatre obliques Un carré ABCD (bleu) de côté
a. Les quatre obliques telles que
AA' avec BA' = x, variable, forment un carré EFGH (jaune). Quelle est la longueur c de
son côté? Et par la même l'aire du
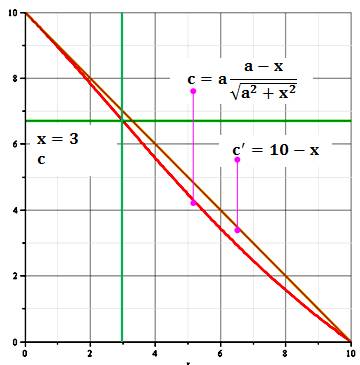
carré jaune. Numérique Ici: a = 10 et x = 3 Les mesures donnent: h = 2,9 et c = 6,8 |
|
||
|
Calcul avec Trigonométrie avec a = 10 et x = 3 |
|||
|
Angle A = angle CBB' |
|
A = 0,29 rad |
|
|
Calcul de h |
h = a sin(A) |
h = 2,873… |
|
|
Avec Pythagore |
c² + 2hc + (2h² – a²) = 0 |
c = 6, 704… |
|
Voir Trigonométrie
|
Calcul formel avec Pythagore et Thalès |
|
|
Avec les triangles
semblables (Thalès)
BFA' et BGC: |
|
|
Dans le triangle rectangle
BCG |
a² = h² + (h + c)² = 2h² + 2hc + c² |
|
Calcul de h (équation du
second degré) |
2h² + 2hc + (c² – a²) = 0 |
|
Racine |
|
|
Côté du carré jaune |
|
|
Solution en c de cette
équation |
|
|
Calcul numérique |
c = 6,704…
et h = 2,873… |
|
Graphe de cette fonction c = f(x) Comparaison avec la droite
(diagonale descendante) |
|
Voir Carré inscrit dans un carré
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()