NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/08/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CARRÉ
Débutants Géométrie	Généralités				Glossaire Géométrie
INDEX Carré Géométrie	Carré	Propriétés	Rigide		Ptolémée
	Carré (suite)	Pavage	Allumette		Carré en 5
	Aire du carré	Carrés dans rectangle		Carrés et cercles
		Carré dans le carré		Partage
		Sommaire de cette page >>> Construction d'un carré avec deux points milieux >>> Un carré ou cinq >>> Dissections >>> Techniques de dissection

Devinette

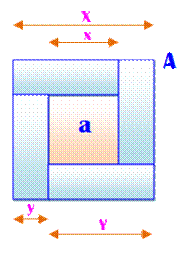
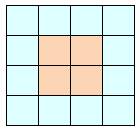
Un carré et quatre rectangles sont ainsi disposés pour former un grand carré. On sait que l'aire du grand carré (A) vaut quatre fois celle du carré interne (a) Quelle est le rapport entre la longueur (Y) de chaque domino et leur largueur (y) ?

Solution

Construction d'un carré
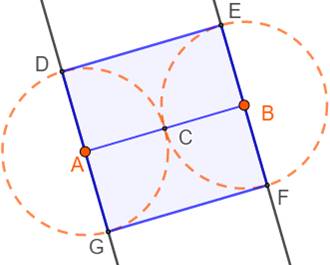
Construire un carré, connaissant deux points milieux A et B. Construction 1. Segment AB et son milieu C 2. Perpendiculaires en A et B à AB 3. Cercles (A, AC) et (B, BC). Intersections D, E, F et G, sommet du carré.

Voir Construction d'un carré passant par quatre points

Un carré ou cinq
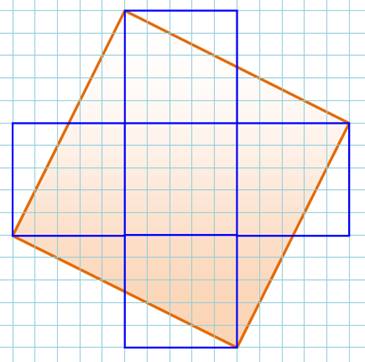
Soit un carré. Comment en quatre lignes (ici en bleu) dessiner cinq petits carrés dont l'aire totale est celle du carré donné (ocre)?

Suite >>>

DISSECTIONS
Dans le cas général, il s'agit de découper une figure pour en former une autre. Un cas fréquent consiste à transformer la figure initiale en carré. Cas célèbre de la chaise à porteur de Sam Loyd, ci-contre. Loyd est la bonne orthographe.	Il s'agit de découper cette forme en deux parties qui, recombinées, forment un carré. Voir Solution
Propriétés Les deux figures ont la même aire (par construction). Tarski, en 1935, a démontré qu'il n'existe pas de dissections paradoxales qui conduiraient à modifier les aires des figures considérées, quelle que soit la complexité du découpage utilisé, sauf pour la sphère. En 1807, William Wallace, puis Bolay et Gerwein, démontrent que, étant donné deux polygones d'aires égales, on peut découper l'un en un nombre fini de pièces qui formeront l'autre. On dit que les polygones de mêmes aires sont équivalents par dissection. Cette propriété n'est pas valable pour les volumes. Un des fameux problèmes de Hilbert (1900) pose la question de l'équivalence des polyèdres de même volume par dissection. En 1901, Max Dehn répond " non ", en prouvant que le cube et le tétraèdre ne sont pas équivalents.

Techniques de dissection
Escalier On peut procéder par tâtonnement, bien sûr; On peut s'aider en considérant trois techniques de base: - Escalier, - Pavage, et - Bande.
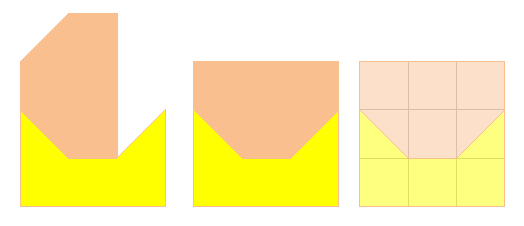
PAVAGE – Dissection de la croix	PAVAGE correspondant
BANDES

Voir Énigme du tapissier / Croix / Dissection du quadrilatère

Maillage de cubes entremêlés

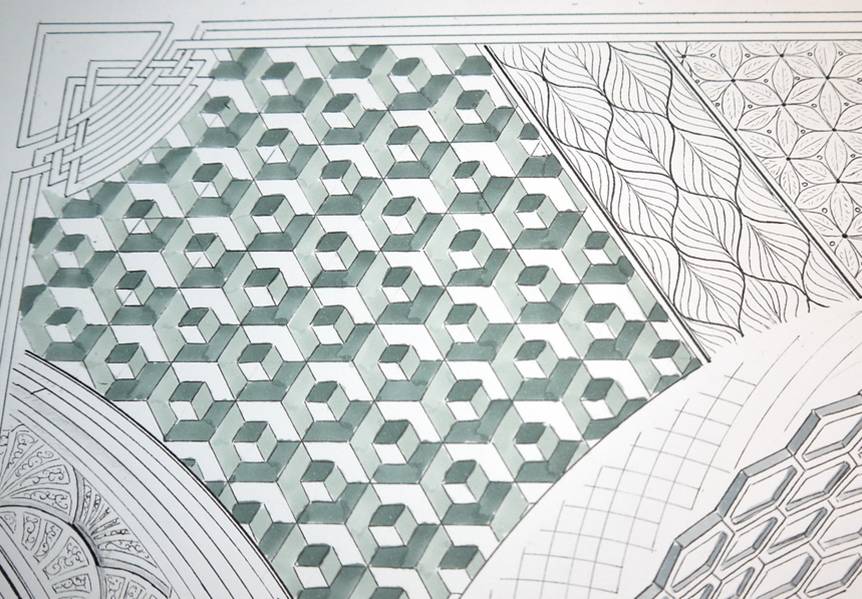
Détail de l'Œuvre de l'artiste Guillaume Villemin (12/19)

Suite	Découpe du rectangle en carré
Voir	Allumettes Allumettes et carrés Carré Carré et nombres complexes Carré manquant Carré rigide Construction à la règle et au compas Construction d'un carré passant par quatre points Cube de Rupert Dissection Énigmes classiques Géométrie Jeux – Index Les trois filles Nombre QUATRE Nombres carrés Pavage de l'échiquier Pavage du carré Pliages Quantité de carrés avec des allumettes Rectangle Topologie – Glossaire
Site	Dissections de polygones
Cette page	http://villemin.gerard.free.fr/GeomLAV/Carre/CarGene.htm

Solution
Dissection Formation du carré Patron Retour

Devinette – Solution

Quelle est le rapport entre la longueur (Y) de chaque domino et leur largueur (y) ? Autre calcul avec les aires

Solution en image

Retour / Autres énigmes / Brève n° 580

Renvoi de lien TÉTRAÈDRE et DOLLAR >>>