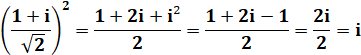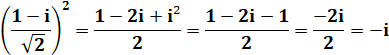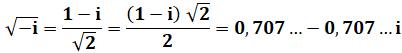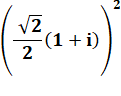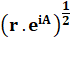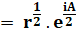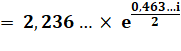|
||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres complexes RACINES La forme polaire se prête aisément au calcul de
la racine nième d'un nombre complexe. |
|
|
|
|
|
Racine carrée de i – Calcul
|
|
||
|
|
(a
+ ib)² |
= i |
|
|
|
a²
– b² + iab |
= i |
|
|
|
a²
– b² 2iab |
= 0 = i |
|
|
|
a 2a² |
= b = 1 |
|
|
|
a
= b |
|
|
|
|
|
= i |
|
|
|
(1 + i) ² |
= 2i |
|
|
|
|||
|
|
|
= ? |
|
|
|
|
= a + ib |
|
|
|
3
+ 4i |
= a² – b² + 2iab |
|
|
|
3 4 |
= a² – b² = 2ab |
|
|
|
b |
= 2/a |
|
|
|
3 |
= a² – 4/a² |
|
|
3a² |
= a4 – 4 |
||
|
0 |
= A² + 3A – 4 |
||
|
|
A1 |
= 1 |
|
|
|
0 |
= (A – 1) (A + 4) |
|
|
|
A2 |
= 4 |
|
|
|
a |
= {1, –1, 2, –2} |
|
|
|
b |
= {2, –2, 1, –1} |
|
|
|
|
= 1
+ 2 i = –1 – 2i = 2
+ i = –2 – i |
|
|
|
(1
+ 2i)² (–1
– 2i)² (2
+ i)² (–2
– i)² |
= 1 – 4 + 4i = –3 +4i = 1 – 4 + 4i = –3 +4i = 4 – 1 + 4i = 3 + 4i = 4 – 1 + 4i = 3 + 4i |
|
|
|
|
= 2 + i ou = –2 – i |
|
Bilan
|
Nous
avons de la chance avec cet exemple car l'équation du second degré est facile
à résoudre. Le calcul en polaire évite ce souci, mais implique une bonne connaissance
de la trigonométrie. Voici la théorie, puis nous reprendrons la résolution du
même exemple. |
|
|
||
|
|
z = a + i .b
|
|
|
|
Autre écriture: |
|
|
|
Soit, autant de racines que de valeurs de k, un nombre
entier. En
résumé
est la racine du module initial.
est l'argument
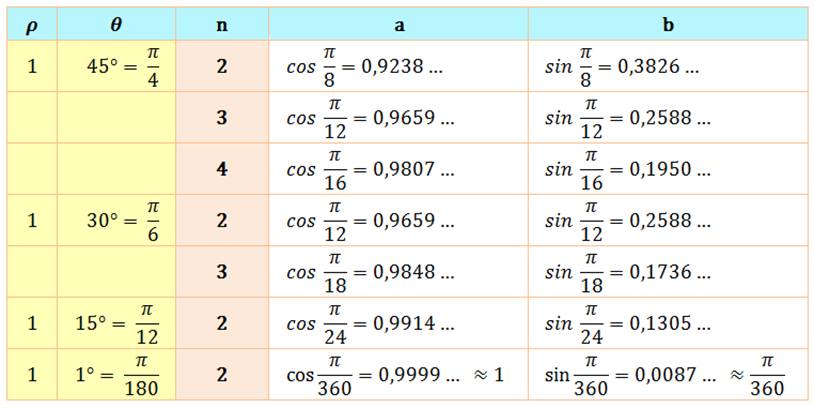
initial divisé par n. Illustration
(valeurs numériques de l'exemple) Le point M' est l'image de la racine du nombre complexe
représenté par M. Le module (r) et l'argument (A) sont calculés ci-dessous)
Notez
bien
La tangente de A est 4/3 et cette de A/2 est ½, pas du tout dans le rapport
des angles ( ½). |
|
|
|||
|
|
|
|
|
|
|
|
= ? |
|
|
|
r |
|
|
|
|
|
= |
|
|
Argument (angle) |
A |
= arctan(4/3) =
0,927… rad = 53,13…° |
|
|
|
A/2 |
= 0,463… rad =
26,56…° Note: la tangente de cet angle en radians est
1/2. |
|
|
|
|
|
|
|
Forme numérique: |
|
|
|
|
|
|||
|
Module |
t |
|
|
|
Argument |
B |
= b / a = 1/2
|
|
|
Expression en b |
|
4b²+ b² = 5
|
|
|
et en a |
|
a = 2 ou –2 |
|
|
|
|
= 2 + i ou = –2 – i |
|
|
|
|
|
Exemples
de lecture:
racine carrée de i = 1 + i; racine carrée de (3 + i) = 1,76 + 0,285 I; etc. Notez les valeurs
entières en jaune, dont notre exemple qui repose sur la propriété du triplet de Pythagore: 3² + 4² = 5². |
|
Voir Tables – Index
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/Racine.htm |
![]()