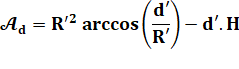|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Chèvre dans un pré circulaire, attachée à l'enclos Cheval, mouton dans le champ, … La chèvre de Poincaré La chèvre est dans un pré,
attachée à une longe. Sans autre indication, elle peut brouter l'herbe sur
une superficie égale à l'aire
du disque. Et quand la corde subit des contraintes ? Objet de nombreuses
énigmes, rarement simples à résoudre. Ici, nous abordons le cas de
l'enclos circulaire, avec longe attachée quelle part sur la clôture. Le
problème passe pour être ardu. Deux solutions sont présentées. Toutes les
deux conduisent à la même équation qui ne peut être résolue que par
itérations. Cette énigme n'est pas
seulement une récréation mathématique. On trouve des applications en
minimisation d'interférences mutuelles, optimisation de la performance des
brouilleurs, calcul de compromis en installation des relais de communication
pour téléphones cellulaires, etc. Première publication connue
de cette énigme en 1748, en Angleterre. |
Anglais: Goat problem / The goat and the barn / Tethered goat
problem /
The Mystery of the Grazing Goat
|
|
|||||
|
La longe
de la chèvre est fixée en périphérie d'un champ circulaire. Quelle
est l'aire abordable par la chèvre? Quelle
est la longueur de la longue telle que cette aire soit égale à la moitié de
l'aire du champ? |
|
||||
|
La première
question consiste à calculer l'aire de la lentille,
intersection entre deux cercles. Avec les
notations de la page de référence: Se référer à cette page sur le calcul de l'aire
de la lentille pour obtenir les formules indiquées ci-dessous. R = 10 et
R' = 7 Avec le
centre du second cercle sur le premier, on a: distance entre centre: H est la
longueur du segment PQ. |
|
||||
|
Mesure de
d |
|
7,55 |
|||
|
Mesure de
d' |
|
2,45 |
|||
|
Mesure de
H |
|
6,55 |
|||
|
Segment
de cercle gauche: |
|
22,00 |
|||
|
Segment
de cercle droit: |
|
43,38 |
|||
|
Aire de
broutage: |
|
65,38977768… |
|||
|
Pas de formule
simple! Pour trouvez quelle est la longueur R' de la longe telle que la surface
à brouter (S) soit moitié de la
superficie à brouter (consigne), on procède par essais successifs (dichotomie). Exemple de calculs progressifs
Avec un cercle de rayon unité et un autre cercle de rayon
r, l'aire de la lentille formée est moitié de celle du disque unité si: Avec 105 chiffres r = 1,1587 2847301812
1517828233 5099335091 4968829226 6492096511 8206958848 2066980255 9196093199 3216107308 6043817596 … |
Merci à Didier
Thonnard pour sa relecture attentive
|
La solution présentée
est générale, même si le point d'attache n'est pas sur l'enclos, mais à
l'extérieur. Il s'agit toujours de calculer l'aire de la lentille formée par
l'intersection de deux cercles. |
|
|
||||
|
Le même
problème. Ici, la solution consiste à trouver une équation à partir de la
lecture d'une figure géométrique, puis à tenter de résoudre cette équation. Après
avoir évalué les angles alpha et béta, on calcule l'aire du secteur jaune,
puis celle du segment bleu. |
|
|||
|
Relation entre
les angles: |
|
alpha = 70,81° béta = 54,59° |
||
|
Aire du secteur
jaune: |
|
Avec R' = 11,58 Aj = 59,75 |
||
|
Aire du segment
bleu: |
|
Avec R = 10 Ab = 19,16 |
||
|
Aire
broutée = 2 x aire de zone colorée: |
|
A = 157,07 Ok compte tenu l'angle alpha
calculé à partir de la solution. |
||
|
Autre manière de présenter l'équation: avec cette identité
sur l'angle moitié. |
|
|
La
formule est plus connue sous cette forme: |
|
Bonus mathématique
|
En
partant de la formule de l'aire de la lentille, on trouve également. Formulation
qui n'est pas plus simple! |
Formule
générale
Formule
adaptée au cas R = D = 1 et en égalant à ½ cercle et
avec R' = x
|
|
Solution
par intégration |
Voir la référence Wikipédia en anglais qui s'intéresse également à
la solution dans l'espace. |
|
Autant il n'est
pas trop compliqué d'obtenir l'équation sous une forme ou une autre, autant
il est difficile de la résoudre. Soit par approche tabulée et dichotomie,
soit par la méthode itérative de Newton, soit avec un logiciel de calcul
comme Maple. |
Voir
Résolution, graphe et
développements trigonométriques autour de cette équation
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette page |
![]()