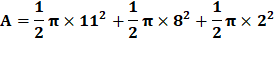|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Chèvre dans un pré avec grange carrée Mouton, cheval … dans le
champ, … La chèvre est dans un pré,
attachée à une longe (une corde ou une chaine). Sans autre indication, elle peut
brouter l'herbe sur une superficie égale à l'aire
du disque. Et quand la corde subit des contraintes ? Objet de nombreuses
énigmes, rarement simples à résoudre. Ici, nous abordons le cas de
la grange de forme carrée, avec la longe qui s'enroule autour de celle-ci. |
Anglais: Goat problem / The goat and the barn / Tethered goat
problem /
The Mystery of the Grazing Goat
|
|
||
|
La chèvre
est en laisse. La corde mesure 8 m. Cette corde est fixée au coin d'une
grange carrée de 4 m de côté. Le cas où
elle est attachée ailleurs sur la grange se traite de la même façon. Quelle
est l'aire broutée par la chèvre? La figure
montre qu'elle a la liberté de brouter:
Ainsi, la
somme est égale à l'aire intérieure à la courbe fermée (qui ressemble à une cardioïde),
à l'exclusion du carré. |
Évidemment la chèvre ne peut pas traverser la grange! Et, la grange
est rigide … |
|
|
Avec la longue longe de 8 m (vert) |
|
|
|
Avec la
longue courte de 4 m (bleu) |
|
|
|
Surface
de liberté de la chèvre |
|
|
|
|
||
|
La longe
est attachée au milieu de la grange (point vert). L'aire
est égale à la somme des aires de trois demi-cercles de rayon 11, 8 et 2
(zones bleues). Lorsqu'on débute, et même ensuite, il est toujours
préférable de vérifier l'ordre de grandeur du résultat: En gros, la zone rose représente le quart de la surface du rectangle.
|
Remarquez la mise en commun de ½ de Pi (on dit: mise en facteur). Le
calcul développé serait:
|
|
Bilan
|
Avec une longe est
plus courte, les quarts de cercle seront
plus petits, mais c'est la même méthode de calcul. Avec une longe
plus longue, la chèvre peut atteindre les
mêmes zones en passant d'un côté ou de l'autre de la grange. La solution est
plus complexe, objet du chapitre suivant. |
|
|
|||
|
Problème Cette
fois la longue est plus longue que deux fois le côté de la grange. Les quarts
de disque en bleu se chevauchent. Il s'agit de retirer cette part qui
doublonne. Dit
autrement: quelle est l'aire de la partie bleue ? Note: le calcul précédent donnerait 93 Pi = 292,17 m², alors que le calcul qui suit
va montrer que la valeur exacte est 288, 53 m². Écart de 3,63 m² (1,25%).
Erreur qui croit avec R. Un longe de 12 m engendrerait un erreur de 5%. |
|
||
|
Démarche Figure et
notations pour calculer l'aire de la zone colorée. On note
bien que les centres des cercles sont en A et B et non pas en O. D'où la
complication. On calcule successivement x, y puis u. Ce qui permet de calculer
l'aire AT du triangle OMC. Avec l'angle alpha, on évalue l'aire AS du segment de
cercle en bleu. L'aire colorée est égale à : Notez que la droite OM est un axe de symétrie et que OQMP est un carré de côté y. |
|
||
|
|
|||
|
Le
segment AB est la diagonale du carré |
|
5,65… |
|
|
La
hauteur du triangle ABM (Th. de
Pythagore) |
|
5,29… |
|
|
Segment
OM: demi-diagonale + hauteur calculée |
|
8,12… |
|
|
Carré
OPMQ |
|
5,74… |
|
|
Aire du triangle
OMC |
|
28,71… |
|
|
Segment AP |
|
1,74 … |
|
|
Angle
alpha |
|
1,2762… radian 73,1255… ° |
|
|
Aire
du segment d'angle alpha |
|
5,75… |
|
|
Aire zone
colorée |
|
52,91… |
|
|
Zone
chèvre (avec la zone verte) |
|
288,532188… |
|
|
Pour information Valeur numérique avec
radicaux
Et la
formule litérale:
|
|||
Bilan
|
Inutile de prendre
la formule littérale complète, le mieux consiste à faire les calculs
numériques pas à pas avec une calculette
ou encore avec un tableur.
|
|
|
||
|
Une
grange (ocre) de 6 m x 4 m. La chèvre
est attachée au piquet vert avec une longe de 15 m. Quelle
est la longueur minimale des clôtures à réaliser (en rouge) pour que la
chèvre reste sur le terrain de 13 m x 16 m. La partie
verticale à gauche mesure évidemment 6 m. La
clôture en haut comprend deux parties: celle interceptée avec un rayon de 5 m
(x1), et celle interceptée avec un rayon de 9 m (x2). |
|
|
|
Théorème de Pythagore dans T1. |
x1² = 5² – 3² = 25 – 9 = 16 => x1 = 4 |
|
|
Théorème
de Pythagore dans T2. |
x2² = 9² – 7² = 81 – 49 = 32 => x1 = 5,656… |
|
|
Longueur
minimale de clôture: |
L = 6 + 4 + 5,656 = 15,656. |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()