|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Le problème de la chèvre dans un champ rectangulaire La chèvre
est dans un champ en forme de rectangle. On se demande
quelle est la longueur de la corde (longe) de sorte que la chèvre peut
brouter exactement la moitié du champ. |
|
|
|||
|
Énigme Le champ
est de forme rectangulaire
et la longe est attachée à un pieu situé au milieu de la largueur. Quelle la
longueur R de la corde pour que la chèvre soit en capacité de brouter
exactement la moitié du champ ? |
|
||
|
La figure annotée Aire
boutée = = 2 x
(jaune + ocre) Quelle
est la valeur de L pour que la chèvre brouet la moitié du rectangle ? |
|
||
|
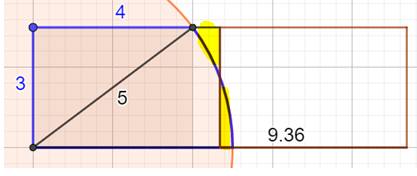
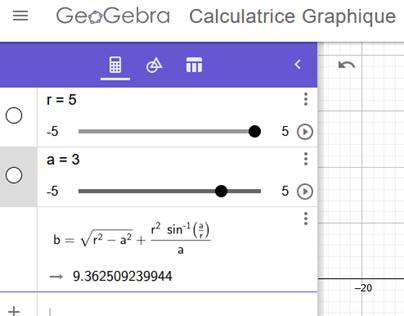
Un exemple de résolution On donne la largeur égale à 6, soit a = 3 et la
longueur de la longe R = 5 On en déduit la longueur du troisième côté du triangle
rectangle: b = 4. |
Avec ces données, la longueur de du champ est 9,36, alors la chèvre broute la moitié du champ. Les surfaces en jaune sont égales. |
||
|
|
|||
|
|
Littéral |
Exemple numérique |
|
|
Aire des deux triangles
rectangles |
|
a = 3 R = 5 => b =
4 AT = 12 |
|
|
Aire
du secteur complet |
|
= 36,87 °
|
|
|
Aire à brouter complète |
|
|
|
|
Aire à brouter |
|
|
|
|
Formule finale |
|
|
|
|
|
||
|
Solutions ? |
Pas de solution analytique ! Impossible de calculer R en connaissant
les dimensions du champ L et 2a. Avec la condition donnée, moitié du champ, la longe doit être assez longue
pour atteindre, en gros, la demi-longueur du champ. La solution consiste à faire un abaque
donnant L pour différentes valeurs de R et a. Ci-dessous un tableau suivi des
courbes. |
|
|
Tableaux de valeurs La valeur 0 indique que ces cas sont impossibles. En rouge, l'exemple numérique traité ci-dessus. |
|
|

|
|
||
|
GDC: graphic display calculator On peut aussi utiliser une calculette
avec résolution graphique d'équations (GDC). Cette fonction est aussi disponible avec GeoGebra en ligne. Exemple de traitement avec
l'exemple numérique de cette page
=> |
|
|
|
Vérification graphique de la formule Cas de a = 10 et R = 10 donnant les aires maximales. Alors L = 15,708. D'ailleurs dans ce cas, on calcule bien:
Sur cette figure avec un contour dessiné à la main, les aires sont
très voisines: 9,13 et 9,01; moyenne 9,07. En prenant l'angle (38,24°) et l'ordonnée du point H (6,19), on
calcule les deux aires par différences. Elles valent: 9,06514528… (évaluation
numérique de la formule ci-contre) |
Chaque aire colorée vaut: |
|
Merci à Jacky P. pour l'idée de cette
page
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()