Bissectrice en trigonométrie, ajouter 1

Édition du: 26/11/2023

INDEX Outils de trigo Trigonométrie Analyse Identités	TRIGONOMÉTRIE
	Débutant	Introduction	Angles	Valeurs
	En pratique	Lignes trigonométriques en bref
	Cours première	Formules	Tangente	Calculs
	Hauteur de l'église	Équations	Calculs simples	Calculs avancés
			Bissectrice (1 ± cos a + i.sin a)

Faites un double-clic pour un retour en haut de page

Bissectrice en trigonométrie

Calcul de z = 1 ± cos(a) + i.sin(a)

La formule avec le signe plus conduit à un angle moitié (bissectrice).

Pour le démontrer, nous allons calculer le nombre complexe z sans la constante 1. Pour cela, il faut calculer le module et l'argument du nombre complexe et repasser sous la forme polaire.

Nous commencerons par des exemples numériques pour approcher le calcul littéral.

Sommaire de cette page

>>> Exemples numériques

>>> Calcul littéral

Débutants

Types de nombres

Glossaire

Nombres complexes

Liens utiles pour cette page

Cercle trigonométrique >>>

Sinus, cosinus, tangente >>>

Valeurs usuelles des sinus et cosinus >>>

Relations trigonométriques >>>

Nombres complexes – Index >>>

Module et argument d'un nombre complexe >>>

Calcul de 1 ± cos(a) + i.sin(a) – Exemple		haut
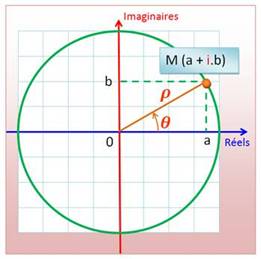
Module et argument d'un nombre complexe La figure permet de rappeler la définition: Module: longueur du segment OM. Il est calculé avec le théorème de Pythagore: Argument: angle de OM par rapport à l'axe des x. Il est calculé via la tangente de l'angle: Exemple avec un angle donné L'exemple numérique développé ci-dessous, permet de se familiariser avec les calculs de modules et d'arguments des nombres complexes. Plus bas, on trouvera la généralisation à un angle quelconque.	a est la partie réelle (Re) du nombre complexe; b est la partie imaginaire (Im) du nombre complexe.
Exemple avec signe négatif un angle de 30°
Exemple avec signe positif et un angle de 60°

Bilan

On retient que pour ce dernier exemple numérique, ajouter 1 dans la partie réelle, entraine un facteur 2 entre les angles aux départ et à l'arrivée.

Est-ce toujours vrai ? C'est l'objet du calcul littéral qui suit.

Calcul de 1 ± cos(a) + i.sin(a)

haut

Cas du signe négatif