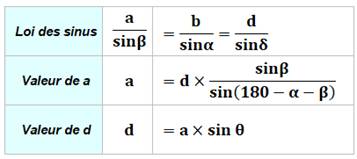Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 14/10/2023 M'écrire Brèves de Maths

INDEX Trigonométrie Analyse	TRIGONOMÉTRIE
	Débutant	Introduction	Angles	Valeurs
	FORMULES	Calculs	Pi/5 = 36°	Cosécante
	Cours première	Tangente	Tangente hyperbolique
		Arctan	Hauteur de l'église

Faites un double-clic pour un retour en haut de page

Hauteur de l'église distante L'église est visible en haut de la colline. Comment estimer sa hauteur ? Où il est question d'un système d'équations pas très sympathique. Comment le résoudre simplement ?
	Sommaire de cette page >>> Église sur la colline >>> Résoudre les équations >>> Hauteur du sommet	Débutants Nombres Glossaire Nombres

Église sur la colline		haut
Observations Une église est visible en haut d'une colline. Comment estimer sa hauteur ? Pistes Nous pouvons mesurer les angles sous lesquels on voit l'église. En un point donné, le sommet est vu sous 40°. En avançant de 100 mètres, son sommet est vu sous 60° et sa base sous 40°. Est-ce suffisant ? Oui ! Des calculs de tangente vont faire l'affaire.
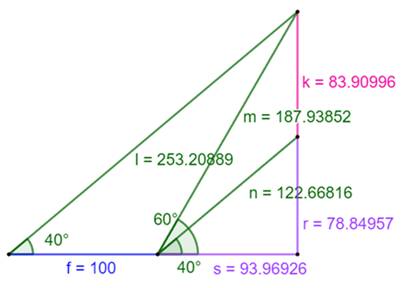
Notation et estimation des tangentes Sur ce plan, nous dessinons un triangle rectangle et les trois angles de vue. On note les segments f, s, r, k. La longueur f est connue (100 m), il nous faut calculer la longueur k. Évaluons les tangentes des angles donnés et notons les a, b et c pour la commodité des calculs.

Résoudre les équations			haut
Calcul des longueurs k, r et s Comment s'y prendre avec ce système d'équations à trois inconnues (k, r et s), composé de fractions ? 1) "déplier" les fractions, et 2) ordonner les variables selon un tableau. La solution devient évidente: 3) soustraire les deux premières équations ce qui élimine les variables k et r. On obtient directement la valeur de s 4) les deux autres en découlent automatiquement.		Tableau simplifiant grandement la résolution des équations
Valeurs numériques Hauteur de l'église: 83, 90 m Située sur une colline de 78,85 m, et à une distance de 93,96 m.	Valeurs confirmées sur le graphique ci-dessus (calculs GeoGebra)

Hauteur du sommet		haut
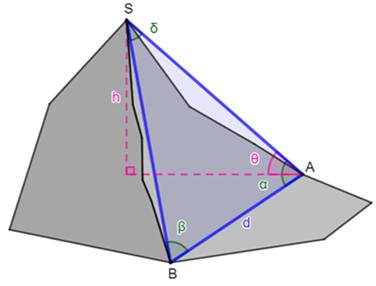
Observations Deux points de mesure A et B, au bas de la montagne. Les altitudes sont différentes. Le sommet S est vu sous les angles alpha et bêta. L'angle d'élévation en A (angle par rapport à l'horizontale) est connu: thêta. On mesure la distance d entre A et B. Quelle est la différence d'altitude h entre A et S ? Pistes Si nous connaissons la valeur de a, nous pouvons calculer la valeur de h dans le triangle rectangle: h = a sin (thêta). Pour connaitre a, essayons d'applique la loi des sinus. En effet on connait un côté (d) et les trois angles du triangle quelconque. Application numérique	Énoncé Notations Exemple numérique

Haut de page (ou double-clic)

Bases	Trigonométrie – Débutant Trigonométrie – Tables Trigonométrie – Identités
Voir	Pente – Calcul de - Tangente – une approche, familiarisation Tangente en géométrie Tangente hyperbolique Tangente pour exprimer une congruence
Aussi	Angles Angles selon leur tangente en dessin Calculs en trigonométrie (avancés) Calculs en trigonométrie (simples) Faire le tour du cercle (relations de base) Identités remarquables Pentagone Sinus et aire du triangle isocèle Triangle
Cette page	http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/TanEglis.htm