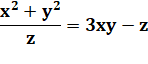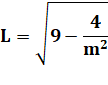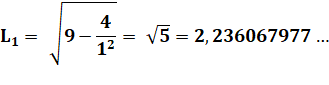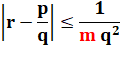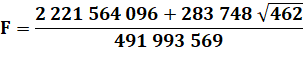|
||||||||||||||||||||||||||||
![]()
|
Nombres de MARKOV Nombres entiers positifs solutions de x² + y² + z² = 3 x y z Une infinité de solutions
dont la construction est originale. Où il est question de
Fibonacci et Pell. Exemple d'une équation de Markov
(1, 2, 5) est un triplet de Markov 1, 2 et 3 sont des nombres e Markov |
Andreï Markov (1856-1922) ou Markoff
Anglais:
Markov numbers
|
|
||
|
Les
premières solutions de l'équation de Markov: Normalisation Les trois
variables x, y et z sont permutables. On ne
considère que les solutions, dites normalisées,
telles que:
|
x² + y² + z² = 3 x y z 1² + 1² + 1² = 3 x 1 x
1 x 1 = 3 1² + 1² + 2² = 3 x 1 x
1 x 2 = 6 1² + 2² + 5² = 3 x 1 x 2 x 5 = 30 1² + 5² + 13² = 3 x 1 x 5 x 13 = 195 |
|
|
=> Triplets
de Markov |
(1, 1, 1) (1, 1, 2) (1, 2, 5) …. |
|
|
=>
Nombres de Markov |
1, 2, 5, 13, … |
|
|
|
||
|
Nombres de Markov |
1, 2, 5, 13, 29, 34, 89, 169, 194, 233, 433, 610, 985, 1 325, 1 597, 2 897, 4 181, 5 741, 6 466, 7 561, 9 077, 10 946, 14 701, 28 657, 33 461, 37 666, 43 261, 51 641, 62 210, 75 025, 96 557, 135 137, 195 025, 196 418, 294 685, 426 389, 499 393, 514 229, 646 018, 925 765, … |
|
|
Triplets de Markov |
1, 1, 1; 3 Les deux premiers triplets sont traités à part; 1, 1, 2; 6 Ce sont les deux
seuls avec des chiffres identiques. 1, 2, 5; 30 1, 5, 13; 195 1, 13, 34; 1 326 1, 34, 89; 9 078 1, 89, 233; 62 211 1, 233, 610; 426 390 2, 5, 29; 870 2, 29, 169; 29 406 2, 169, 985; 998 790 5, 13, 194; 37 830 5, 29, 433; 188 355 … |
|
|
|
||
|
Distincts Les trois
entiers d'un triplet de Markov sont distincts, sauf pour les deux premiers. Dans un
triplet de Markov, deux valeurs sont communes à trois autres triplets. |
Unicité On conjecture
que: pour un nombre de Markov z donné, il n'existe qu'une seule solution
normalisée, z étant le plus grand nombre du triplet. => Il
n'existerait pas deux triplets tels que: À ce jour (2017), la conjecture n'est que partiellement
démontrée. |
|
|
Propagation – Filiation Si (x, y,
z) est un triplet de Markov, Il existe
donc une infinité de nombres de Markov. En effet: x² + y² + (3xy – z)² = 3xy (3xy – z) x² + y² + 9x²y² – 6xyz + z² = 9x²y² –
3xyz x² + y² + z² = 3xyz |
(1, 2, 5) => (1, 2, 6 – 5) = (1, 1, 2) (1, 5, 13) => (1, 5, 15 – 13) = (1, 2, 5) |
|
|
Relation
|
Exemple (1, 2, 5) => (1² + 2²) / 5
= 1 et 3x1x2 – 5 = 1 |
|
|
Triplet de Markov-Fibonacci et Triplets de Markov-Pell |
(1, F2n – 1 , F2n
+ 1 ) (2, P2n – 1 , P2n
+ 1 ) >>> |
|
|
Divers
Qui n'a pas de solution pout A > n |
||
|
|
|
|
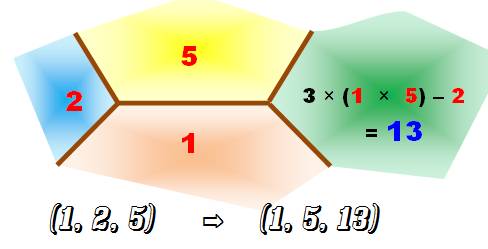
Avec la formule de propagation,
construction d'un nouveau nombre de
Markov: (x, y, z) devient (x, y, 3xy
– z) Avec le
triplet normalisé (1, 2, 5), on construit le nouveau nombre de Markov: 13 Et le
nouveau triplet de Markov: (1, 5, 13)
Règle Prendre
deux nombres de régions contigües pour x et y (1 et 5) et prendre le nombre
de la région "en arrière" pour z (2). Faire l'opération 3xy – z.
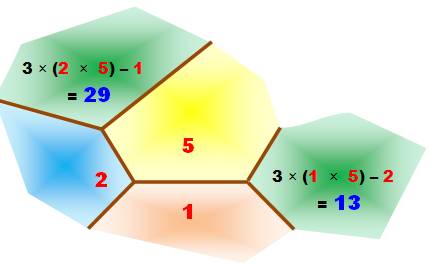
Puis ordonner par nombres croissants (normalisation). Poursuite de l'exemple Avec la
construction du nombre 29 et du triplet (2, 5, 29)
Filiation Sauf pour
les deux premiers triplets, tout triplet a exactement deux "fils": (x, y, z) => (x, z,
3xz – y) et (y, z, 3yz – x) (1, 2, 5) => (1, 5,
13) et (2, 5, 29) Construction
des premiers triplets selon cette filiation:
|
|
|
|
||
|
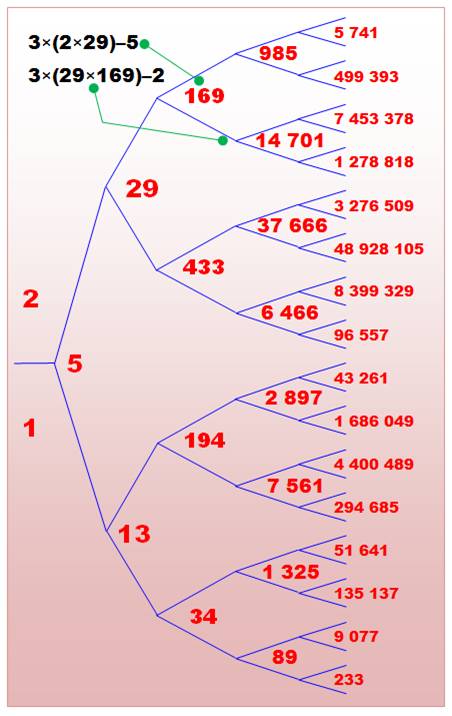
Construction des cinq premiers
étages de l'arbre de Markov En noir
(haut-gauche), deux exemples de calcul. Trois
nombres de zones contigües forment un
triplet, comme: (1, 2, 5;
30), (1, 34, 89; 9 078), (2, 29, 169;
29 406) ou (29, 169, 14 701; 216 148 803). Propriétés Markov a
démontré que cette méthode construit tous les nombres de Markov. Tous les
nombres de cet arbre sont uniques, ce qui tendrait à confirmer la conjecture
d'unicité. La branche du bas est faite des nombres de Fibonacci,
un sur deux: La
branche du haut est faite des nombres de Pell,
un sur deux: 2, 5, 12, 29, 70, 169, 408, 985, 2 378,
5 741, 13 860, 33 461,
80 782, 195 025, 470 832, … |
|
|
|
|
||
|
Les nombres de Markov sont utilisés dans la
théorie de l'approximation rationnelle des nombres irrationnels. |
||
|
Nombres de Lagrange
|
|
|
|
Lagrange a démontré
qu'il existe une infinité d'approximations p/q d'un nombre réel r tel que: |
|
|
|
Avec
certaines hypothèses, le degré d'approximation peut être affiné avec les
nombres de Markov successifs. |
|
|
|
Cette théorie
fait également intervenir le nombre de Friedman. Tous les
nombres réels supérieurs à cette valeur sont approximables par l'inégalité de
Lagrange. |
|
|
Voir
Réduites
des principales constantes / Autres
nombres de Friedman
![]()
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Site |
|
|
Cette page |
![]()