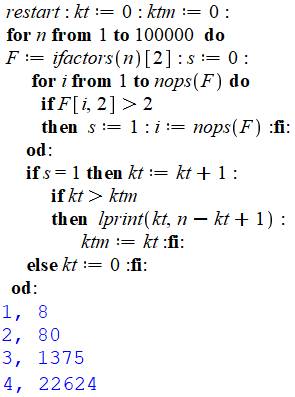|
|||||||||||||||||||||||||||||
![]()
Nombres
sans facteur cube
|
F |
Nombre / Diviseurs / Multiplicatif / Composé /
Seul / |
|
Définitions |
Nombre
non divisible par un cube. Nombre
qui, dans sa décomposition en facteurs premiers, ne possède pas de facteur
élevé au cube. Aucun des exposants n'est supérieur à 2. |
|
Exemples |
Sans cube: 100 = 22 x 52 Avec cube: 108 = 22 x 33 |
|
Anglais |
Cube-free
numbers |
|
Voir |
|
|
|||||||||
|
Nombre SANS facteur cube (cube-free) 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20,
21, 22, 23, 25, 26, 28, 29, 30, 31, 33, 34, 35, 36, 37, 38, 39, 41, 42, 43,
44, 45, 46, 47, 49, 50, 51, 52, 53, 55, 57, 58, 59, 60, 61, 62, 63, 65, 66,
67, 68, 69, 70, 71, 73, 74, 75, 76, 77, 78, 79, 82, 83, 84, 85, 86, 87, 89,
90, 91, 92, 93, 94, 95, 97, 98, 99, 100, … |
Nombre AVEC facteur cube (cubeful) 8, 16, 24,
27, 32, 40, 48, 54,
56, 64, 72,
80, 81, 88,
96, 104, 108, 112,
120, 125, 128,
135, 136, 144,
152, 160, 162,
168, 176, 184,
189, 192, 200, 208,
216, 224, 232,
240, 243, 248,
250, 256, 264,
270, 272, 280,
288, 296, 297, 304,
312, 320, 324,
328, 336 … |
||||||||
|
Quantité de nombres
SANS facteur cube
|
|||||||||
|
|
||
|
Programme expert
|
Ce
programme produit la liste des nombres sans cube et celle des nombres avec
cubes. Il
utilise des notions avancées en programmation Maple Commentaires Procédure
de détermination si un nombre est sans cube. L'instruction
ifactors(320), par exemple, retourne les
facteurs sous cette forme: [1,
[[2, 6], [5, 1]]]. On examine seulement la deuxième composante [2, 6], [5,
1]] avec ifactor(n)[2]. Dans
cette composante, on s'intéresse au deuxième nombre de chaque liste op(2,p). Si
l'un d'entre eux est supérieur à 2, alors il existe un cube et la réponse est
fausse, sinon elle est vraie. Le
programme principale déroule une boucle d'exploration et remplit une liste
pour les nombres sans cube et une autre pour les nombres avec cube. En
bleu, un exemple de résultat de traitement. |
|
|
Programme classique
|
Ce
programme produit la liste de records de
suite de kt nombres consécutifs avec cubes. Programmation
conventionnelle, sans astuce particulière. Commentaires Le
compteur kt compte les occurrences successives de nombres avec cubes. ktm enregistre
les records de longueur de kt. Boucle
de recherche de 1 à 100 000. F
contient le deuxième élément [2] de l'ensemble des facteurs (voir
explications ci-dessus). Un
témoin de présence de cube s est mis à zéro. Si
l'un des exposants F[i,2] est un cube ou plus, le témoin s le signale en
passant à 1 et on arrête la boucle en imposant que i prenne la valeur max. En
cas de nombre avec cube (s =1), le compteur est incrémenté. Si la valeur surpasse
le record ktm, on imprime la valeur de n du début de suite et le record prend
une nouvelle valeur. Si le nombre n'est pas avec cube, le compteur est remis
à zéro. |
|
Voir Programmation – Index
Voir DicoNombre: 48, 80, 242, 844,
1 215,
1 375,
22 020,
22 624,
33 614
/ Détails
pour les squareful (p = 2)
|
Listes particulières |
|
|
|
Record de
nombres consécutifs avec carrés. En rose, rappel des nombres du tableau
ci-dessus. Exemple: 48 = 24 x 3; 49 = 72 ; 50 = 2 x 52 OEIS - A045882 - Smallest term of first
run of (at least) n consecutive integers which are not squarefree. |
4, 8, 48, 242, 844, 22020, 217070,
1092747, 8870024, 221167422, 221167422, 47255689915, 82462576220,
1043460553364, 79180770078548, 3215226335143218, 23742453640900972,
125781000834058568, … |
|
|
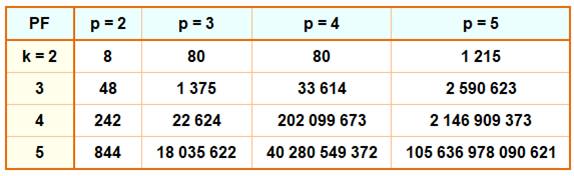
Record de
nombres consécutifs avec cube. En rose, rappel des nombres du tableau
ci-dessus. Exemple: 80 = 24 x 5; 81 = 34 OEIS – A271443 – Earliest start of a run
of n numbers divisible by a cube larger than one |
8, 80, 1375, 22624, 18035622,
4379776620, 1204244328624, 2604639091138248, 2604639091138248, … |
|
![]()
|
Voir |
|
|
DicoNombre |
|
|
Livre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPMULTI/Cubefree.htm
|