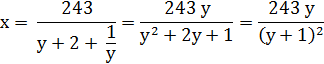|
|||||||||||||||||||||||||||||||||||
![]()
|
Nombres
QUATROPS et
les quatre opérations Énigme
impliquant addition,
soustraction, multiplication
et division de deux nombres. Ex:
243 = (24+8) + (24-8) + (24x8) + (24/8) = (54+2) + (54-2) + (54x2) + (54/2) Généralisation
aux nombres "quatrops" (quatre
opérations). Une partition
particulière des nombres. Où l'on redécouvre les multiples des nombres carrés et les nombres sans facteur carré. |
Voir
Nombres
quatrops – Débutants
|
|
|
|
On convient que x > y, sans que cela change la
nature de la question. 243 = (x
+ y) + (x – y) + (x . y) + (x / y) 243 = 2x
+ x.y + x/y = x (2 + y + 1/y)
La dernière étape utilise une identité remarquable.
243 = 9 x 27; et 27 = 33; soit: 243 = 32
x 33 = 35.
y = 0
=> x = 243 x 0 / 1² impossible y = 2 => x = 243 x 2 / 3² = 54 y = 8 =>
x = 243 x 8 / 9² = 24 L'auteur de cette énigme est: Roger La Ferté |
|
Voir Puissance
|
|
|
|
Il suffit que N = k (y + 1)² pour que cette énigme
marche. Exemple: y = 6;
(y + 1)² = 49 => x = 49k x 6/7² avec k = 9, par exemple, voici l'énigme:
On remarque que 441 est divisible par 9: 441 = 9 x
49 = 9 x 7² Diviseurs carrés de 441: 3 et 7 => y = 2 ou 6. y = 2 =>
x = 441 x 2 / 3² = 98 y = 6 =>
x = 441 x 6 / 7² = 54
Pour x = 9 et y = 9, N = 10² =
100. Pour x = 27 et y = 9, N = 27 x 100 / 9 = 300 |
|
|
|
|
|
|
|
Suite Table jusqu'à 250
|
|
|
|
Carrés Un nombre carré peut toujours s'écrire sous la forme de la somme des
résultats des quatre opérations sur le même
nombre: C = (a+a)
+ (a-a) + (a.a) + (a/a) = a²+ 2a + 1 = (a+1)² Voir Nombres carrés / Identité remarquable Nombres
en 4k et 1 Tous les nombres divisibles par 4 (N = 4k) sont de la forme : N = (k+1)
+ (k-1) + (k.1) + (k/1) = 4k Voir Divisible par 4 Nombres
en 9k et 2 Tous les nombres divisibles par 9 (N = 9k) sont de la forme : N = (2k+2)
+ (2k-2) + (2k.2) + (2k/2) = 9k Voir Divisible par 9 Nombres
en 16k et 3 Tous les nombres divisibles par 16 (N = 16k) sont de la forme : N = (3k+3)
+ (3k-3) + (3k.3) + (3k/3) = 16k Nombres
en (c+1)² . k et c Tous les nombres divisibles par (c+1)², soit N = (c+1)²k, sont de la forme
: N = (k.c+c) + (k.c-c)
+ (k.c.c) + (k.c/c) =
(c+1)².k |
|
|
En
bilan, les nombres QUATROPS
sont tous les MULTIPLES DES CARRÉS. En remarquant que les quantités de
présentations dans les deux cas sont égales. Exemple: 16 = 4² = 4 x 2² => 2 présentations,
et 16 = (4+1) + (4-1) + (4x1) + (4/1) =
(3+3) + (3-3) + (3x3) + (3/3) => 2 présentations. Les nombres
non-quatrops sont en fait les nombres sans carré (square-free). |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()