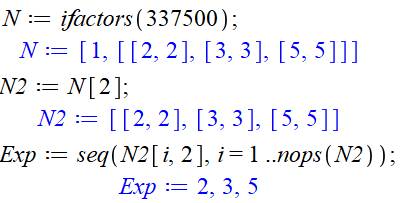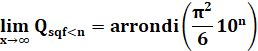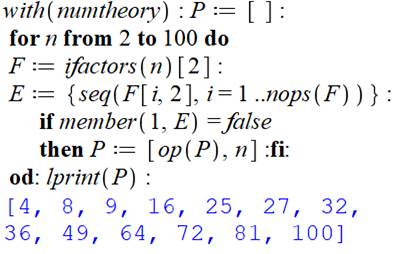|
|||||||||||||||||||||||||||||
![]()
|
Famille |
Nombre / Diviseurs / Multiplicatif / Composé /
Seul / |
|
|
Approche |
Illustration
|
|
|
Définitions |
Aucun
des exposants n'est supérieur à 1. Tous
les facteurs sont distincts. |
|
|
Propriétés |
les
nombres premiers, et les
nombres simples et
le nombre 1 par pure définition.
La
densité asymptotique est donc de 6 / p² = 0, 607 927 … |
|
|
Applications |
|
|
|
Exemples |
OUI 6 = 1 x 2 x 3 7 = 1 x 7 105
= 1 x 3 x 5 x 7 106
= 2 x 53 107
= 1 x 107 |
NON 4 = 2² 8 = 23 20 = 2² x 5 40 = 23
x 5 120
= 1 x 2 x 3 x 4 x 5 = 5! |
|
Anglais |
|
|
|
Espagnol |
|
|
|
|
|
|
Record avec huit nombres à facteurs carrés successifs
Record avec neuf: 8
870 024; dix et onze: 221 167 422; douze: 45 255 689 915 Référence pour ces trois cas:
Those
fascinating numbers – Jean-Marie De Koninck
|
|
Voir DicoNombre: 48, 242, 844,
22 020
/ Brève
n° 414
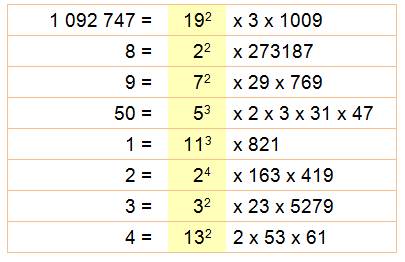
Extension aux puissances supérieures
|
En
colonne 2, on retrouve (comme
ci-dessus) les records de quantité de nombres successifs avec une
puissance de 2. Même
chose pour les colonnes suivantes avec les puissances de 3 à 5.
Exemple: 80 = 24 x 5 et 81 = 34,
éligible pour p = 3 et p = 4. |
Voir Nombres
sans cube (cube-free)
![]()
|
|
||
|
|
Cas où on ne dispose que de la factorisation Principe de l'extraction des exposants L'instruction ifactors
produit la liste des facteurs en identifiant le 1 en tête Nous voulons le deuxième élément de la liste N2. De cette liste nous voulons extraire le deuxième
élément de chaque couple N2[i,2] pour i
allant de 1 au dernier élément: nops(N2). |
|
|
|
Commentaires aux logiciels de théorie des nombres. Procédure (sous
–programme) indiquant si un nombre est sans carré (sqf = 1). Identification des facteurs de n en N. Boucle en i de recherche des exposants supérieurs
à 1, ce qui indiquerait que le nombre n'est pas sans carré. Arrêt (break) dès qu'un tel exposant est trouvé. La procédure retourne sqf = 1 si le nombre est
sans carré et 0 sinon. Le programme principal explore n de 2
à 1 million et forme la liste N des nombres sans carré, puis la liste M des
nombres sans carré au rang des puissances de 10 successives. Attention les temps de calculs sont très longs
(heures!). |
|
|
|
Plus
simple avec factorset Maple dispose d'une instruction qui liste les facteurs. Leur
multiplication donne le radical Si le nombre est égal au radical, il est sans carré. |
|
|
Encore plus
simple avec issqrfree Maple
dispose d'une instruction qui identifie les nombres sans carré. |
Voir Programmation – Index
![]()
Tables
Nombres sans facteur
carré de rang 10 puissance kième
|
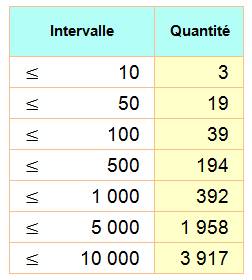
Quantité asymptotique
Valeurs exactes (et selon formule) 10 => 15 (16) 100 => 163 (164) 1000 => 1 639 (1 645) |
104
=> 16 447 (16 449) 105
=> 164 449 (164 493) 106
=> 1 644 919 (1 644 934) 107
=> 16 449 370 (16
449 341) 108
=> 164 493 391 (164 493 407) 109
=> 1 644 934 082 (1
644 934 097) |
Liste
des nombres sans facteur carré
jusqu'à
1010 (square-free)
|
1, 2,
3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, 31,
33, 34, 35, 37, 38, 39, 41, 42, 43, 46, 47, 51, 53, 55, 57, 58, 59, 61, 62,
65, 66, 67, 69, 70, 71, 73, 74, 77, 78, 79, 82, 83, 85, 86, 87, 89, 91, 93,
94, 95, 97, 101, 102, 103, 105, 106, 107, 109, 110, 111, 113, 114, 115, 118,
119, 122, 123, 127, 129, 130, 131, 133, 134, 137, 138, 139, 141, 142, 143,
145, 146, 149, 151, 154, 155, 157, 158, 159, 161, 163, 165, 166, 167, 170, 173, 174, 177, 178, 179, 181, 182, 183,
185, 186, 187, 190, 191, 193, 194, 195, 197, 199, 201, 202, 203, 205, 206,
209, 210, 211, 213, 214, 215, 217, 218, 219, 221, 222, 223, 226, 227, 229,
230, 231, 233, 235, 237, 238, 239, 241, 246, 247, 249, 251, 253, 254, 255,
257, 258, 259, 262, 263, 265, 266, 267, 269, 271, 273, 274, 277, 278, 281,
282, 283, 285, 286, 287, 290, 291, 293, 295, 298, 299, 301, 302, 303, 305,
307, 309, 310, 311, 313, 314, 317, 318, 319, 321, 322, 323, 326, 327, 329,
330, 331, 334, 335, 337, 339, 341, 345, 346, 347, 349, 353, 354, 355, 357,
358, 359, 362, 365, 366, 367, 370, 371, 373, 374, 377, 379, 381, 382, 383,
385, 386, 389, 390, 391, 393, 394, 395, 397, 398, 399, 401, 402, 403, 406,
407, 409, 410, 411, 413, 415, 417, 418, 419, 421, 422, 426, 427, 429, 430,
431, 433, 434, 435, 437, 438, 439, 442, 443, 445, 446, 447, 449, 451, 453,
454, 455, 457, 458, 461, 462, 463, 465, 466, 467, 469, 470, 471, 473, 474,
478, 479, 481, 482, 483, 485, 487, 489, 491, 493, 494, 497, 498, 499, 501,
502, 503, 505, 506, 509, 510, 511, 514, 515, 517, 518, 519, 521, 523, 526,
527, 530, 533, 534, 535, 537, 538, 541, 542, 543, 545, 546, 547, 551, 553,
554, 555, 557, 559, 561, 562, 563, 565, 566, 569, 570, 571, 573, 574, 577,
579, 581, 582, 583, 586, 587, 589, 590, 591, 593, 595, 597, 598, 599, 601,
602, 606, 607, 609, 610, 611, 613, 614, 615, 617, 618, 619, 622, 623, 626,
627, 629, 631, 633, 634, 635, 638, 641, 642, 643, 645, 646, 647, 649, 651,
653, 654, 655, 658, 659, 661, 662, 663, 665, 667, 669, 670, 671, 673, 674,
677, 678, 679, 681, 682, 683, 685, 687, 689, 690, 691, 694, 695, 697, 698,
699, 701, 703, 705, 706, 707, 709, 710, 713, 714, 715, 717, 718, 719, 721,
723, 727, 730, 731, 733, 734, 737, 739, 741, 742, 743, 745, 746, 749, 751,
753, 754, 755, 757, 758, 759, 761, 762, 763, 766, 767, 769, 770, 771, 773,
777, 778, 779, 781, 782, 785, 786, 787, 789, 790, 791, 793, 794, 795, 797,
798, 799, 802, 803, 805, 806, 807, 809, 811, 813, 814, 815, 817, 818, 821,
822, 823, 826, 827, 829, 830, 831, 834, 835, 838, 839, 842, 843, 849, 851,
853, 854, 857, 858, 859, 861, 862, 863, 865, 866, 869, 870, 871, 874, 877, 878,
879, 881, 883, 885, 886, 887, 889, 890, 893, 894, 895, 897, 898, 899, 901,
902, 903, 905, 906, 907, 910, 911, 913, 914, 915, 917, 919, 921, 922, 923,
926, 929, 930, 933, 934, 935, 937, 938, 939, 941, 942, 943, 946, 947, 949,
951, 953, 955, 957, 958, 959, 962, 965, 966, 967, 969, 970, 971, 973, 974,
977, 978, 979, 982, 983, 985, 986, 987, 989, 991, 993, 994, 995, 997, 998,
1001, 1002, 1003, 1005, 1006, 1007, 1009, 1010 … |
Liste des nombres premiers >>>
Liste de nombres simples >>>
Liste
des nombres AVEC facteur carré
(non square-free)
|
Nombres dont un
des facteurs au moins est à une puissance supérieure à 1. Ces nombres sont
divisibles par un carré (critère simple pour leur recherche par
programmation). 4,8,9,12,16,18,20,24,25,27,28,32,36,40,44,45,48,49, 50,52,54,56,60,63,64,68,72,75,76,80,81,84,88,90,92,96,98,99, 100,104,108,112,116,117,120,121,124,125,126,128,132,135,136,140,144,147,148, 150,152,153,156,160,
… La
suite se lit en prenant les nombres qui ne sont pas dans la liste ci-dessus. En jaune les triplets de nombres successifs avec carrés. La liste: 48, 98,
124, 242, 243, 342, 350, 423, 475, 548, 603, 724, 774, 844, 845, 846 … Quadruplets: 242, 844, 845, 1680, 1681, 2888, 2889, 3174,
3624, 3625, 3750, 5046, 5047, 8475, 8523, 8954 … Quintuplets: 844, 1680, 2888, 3624, 5046 …. Voir Plages ci-dessus Quantité de nombres sans carrés
Propriété Les deux seuls
nombres avec facteurs carrés de la forme n3 + 1 sont: 9 = 32 = 23 + 1 12 168 = 23 x 32 x 132 = 233 + 1 |
Plages de nombres divisibles par un carré.
|
2:
8, 24, 27, 44, 63, 75, 80, 116, 120, 135,
147, 152, 168, 171, 175, 188, 207, 224, 260, 275, 279, 288, 296, 315, 324, 332,
360, 363, 368, 375, 387, 404, 440, 459, 495, 507, 512, 524, 528, 531, 539,
567, 575, 584, 620, 624, 636, 639, 656, 675, 692, 711, 728, 735, 747, 764,
783, 800, 819, 824, 832, 836, 840, 855, 867, 872, 875, 891, 908, 924, 927,
931, 944, 960, 963, 975, 980, … 3: 48, 98, 124, 342,
350,
423, 475, 548,
603,
724, 774,
1024, 1250, 1274, 1323, 1375, 1420, 1448, 1519, 1664, 1674, 1848, 1862, 1924,
2007, 2023,
2056, 2106, 2150, 2223, 2275, 2348, 2366, 2523, 2527, 2574, 2644, 2824, 2871,
3050, 3123, 3184, 3211, 3248, 3283, 3428, 3474, 3479, 3508, 3548, 3575, 3608,
3698, 3716, 3724, 3771, 3870, 3950, 4023, 4075, 4112, 4148, 4203, 4374, 4418,
4475, 4598, 4624, 4804, 4850, 4912, 4923, 4948, 4959, 4975, 5192, … 4: 242,
3174, 3750, 8475, 8523, 8954, 10050, 10827, 11322, 13374, 15775, 16575,
19647, 20574, 21462, 22382, 22831, 23762, 23823, 24450, 26702, 26874, 27547,
28322, 28518, 28674, 29887, 30723, 31407, 31974, 34347, 35450, 35574, 35622,
37386, 39050, 39347, 40050, 41742, 45123, 45175, 46023, 48222, 49147, … 5: 844,
1680, 2888, 3624, 5046, 10924, 14748, 15848, 17404, 19940, 22624, 23272,
25772, 29348, 30248, 33172, 36700, 37248, 38724, 39444, 40472, 45372, 47724,
47824, 48372, 49488, … 6: 22020,
24647, 30923, 47672, … 7: 217070,
… 8:
1092747, … |
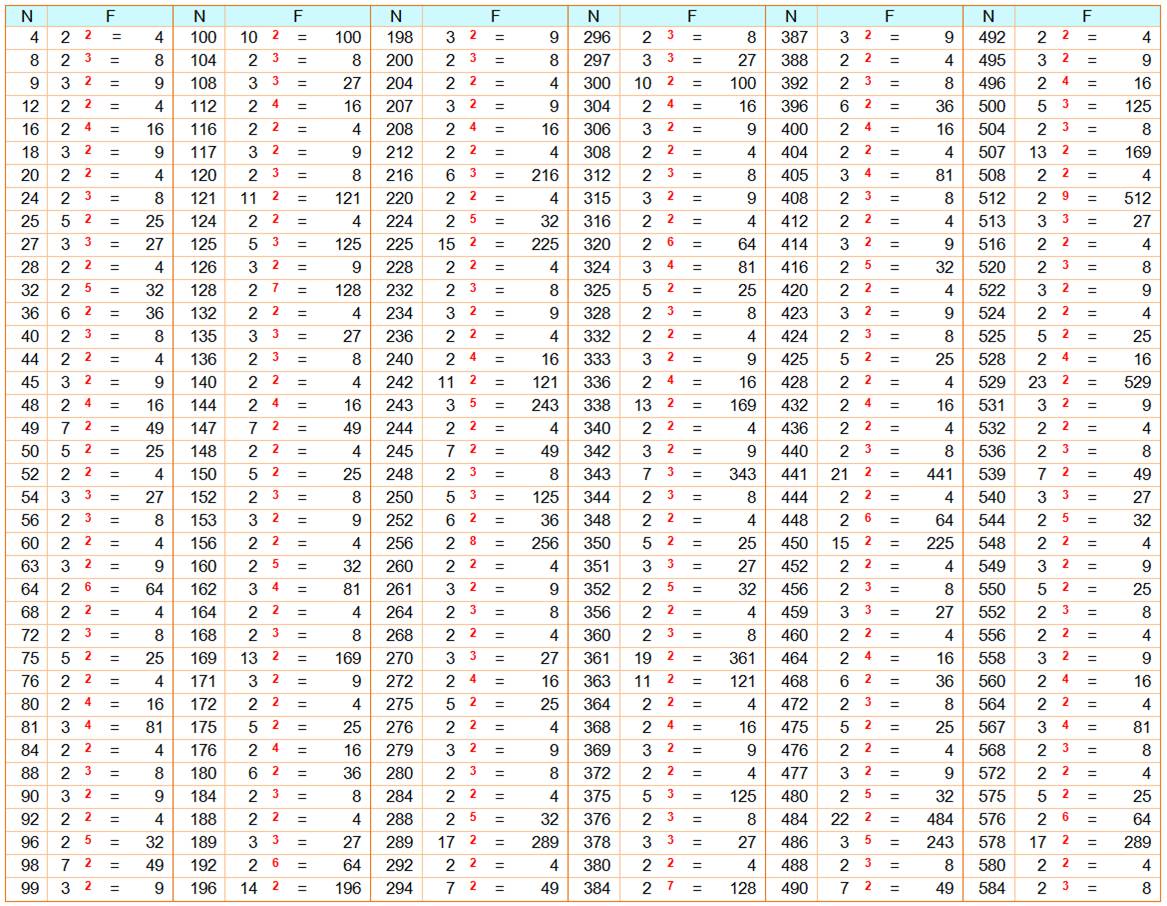
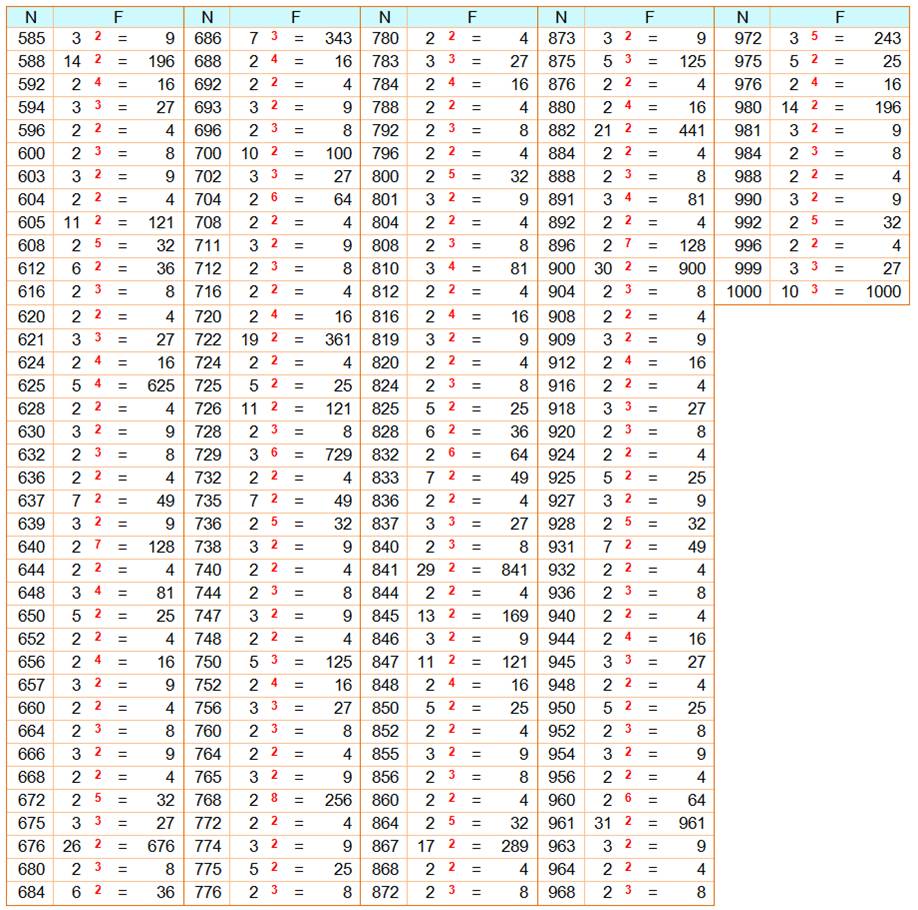
Nombre (N) 1 à 1000 AVEC facteur carré (F) mentionné
F est en fait la puissance égale ou supérieure à 2.
Liste
des nombres PUISSANTS ou plénipotents
(Powerfull numbers or squarefull
numbers)
|
Nombres dont tous
les facteurs sont à une puissance supérieure à 1. 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 72, 81, 100, 108, 121, 125, 128,
144, 169, 196, 200, 216, 225, 243, 256, 288, 289, 324, 343, 361, 392, 400,
432, 441, 484, 500, 512, 529, 576, 625, 648, 675, 676, 729, 784, 800, 841,
864, 900, 961, 968, 972, 1000, 1024, 1089, 1125, 1152, 1156, 1225, 1296,
1323, 1331, 1352, 1369, 1372, 1444, 1521, 1568, 1600, 1681, 1728, 1764, 1800,
1849, 1936, 1944, 2000, 2025, 2048, 2116, 2187, 2197, 2209, 2304, 2312, 2401,
2500, 2592, 2601, 2700, 2704, 2744, 2809, 2888, 2916, 3025, 3087, 3125, 3136,
3200, 3249, 3267, 3364, 3375, 3456, 3481, 3528, 3600, 3721, 3844, 3872, 3888,
3969, 4000, 4096, 4225, 4232, 4356, 4489, 4500, 4563, 4608, 4624, 4761, 4900,
4913, 5000 |
|
|
|
Ouverture
des logiciels de théorie des nombres. préparation de la liste P des nombres
puissants. Boucle de recherche avec les nombres n de 2
à 100. Les facteurs de n (F) se trouvent dans le
deuxième élément de ifactor. Là, on isole (E) le deuxième élément
(l'exposant de la puissance) de chaque
facteur énoncé dans S. S'il n'existe pas d'exposants égaux à 1,
alors on place ce nombre dans la liste des puissants. Fin de boucle et impression. |
Voir Nombres plénipotents ou puissants / Programmation – Index
![]()
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPMULTI/Squarefr.htm |