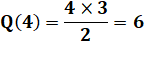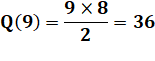Quantité de droites entre 2 points sur une grille

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/11/2020 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	DROITES
Débutants Géométrie	Passant par k points				Glossaire Géométrie
INDEX GÉOMÉTRIE Dénombrement	Droites par n points		Diagonales polygones	Segments dans les objets
	Segments dans grille		Grille: droites par 2 points	Grille: droites par 3 points
	Obliques dans une grille
		Sommaire de cette page >>> Grille 2x2 >>> Grille 3x3 >>> Grille 4x4 >>> Quantité de lignes – Grille (4, 4) >>> Table des valeurs

Quantité de droites passant par deux points

sur une grille k x k

Une grille régulière de points. Combien peut-on dessiner de droites passant par deux points? Soit deux points exactement ou deux points ou plus.

Grilles 2x2

On sait compter la quantité de droites qui relient quatre points quelconques:

Sur la grille régulière 2 x 2, on dénombre effectivement:

2 droites horizontales

2 droites verticales => HV = 2 x 2

1 droite oblique gauche, et

1 droite oblique droite => O = 2 x 1.

Tableau résumant ce cas

Grille	T∀	HV	O	T2
2 × 2	6	2 × 2	2 × 1	6

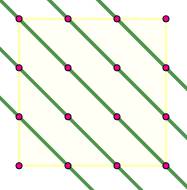
Six droites passant par 2 points

sur cette grille 2 x 2.

Grilles 3x3

Quantité de droites qui relient neuf points quelconques:

Par 2 points ou plus

Sur la grille régulière 3 x 3, on dénombre:

2 x 3 horizontales et verticales (bleues)

2 x 3 obliques dans grille 1x1 (vertes)

4 x 2 obliques dans grille 1x2 (rouges).

Tableau résumant ce cas

Grille	T∀	HV	O11	O12	T2
3 × 3	36	2 × 3	2 × 3	4 x 2	20

Par 2 points exactement

Sur la grille régulière 3 x 3, on dénombre:

0 horizontales et verticales

2 x 2 obliques dans grille 1x1 (vertes)

4 x 2 obliques dans grille 1x2 (rouges).

Tableau résumant ce cas

Grille	T∀	HV	O11	O12	T2
3 × 3	36	0	2 × 2	4 x 2	12

Grilles 4x4

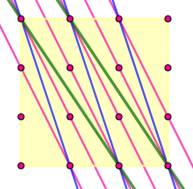
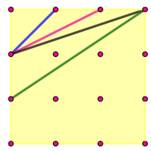
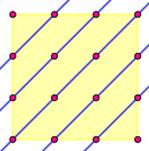
Quantité de droites qui relient seize points quelconques:

Par 2 points

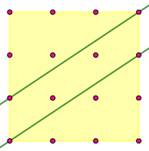
Non représenté: 2 x 4 horizontales et verticales dont 0 par 2 points exactement: HV = (2x4, 0)

Vert: 2 x 5 obliques par les grilles 1x1 dont 2 x 2 par 2 points exactement: O11 = (2x5, 2x2)

Rouge: 4 x 6 obliques par les grilles 1x2 dont tous par 2 points exactement: O12 = (4x6, 4x6)

Bleu: 4 x 3 obliques par les grilles 1x3 dont tous par 2 points exactement: O13 = (4x3, 4x3)

Vert: 4 x 2 obliques par les grilles 2x3 dont tous par 2 points exactement: O13 = (4x2, 4x2)

Tableau résumant ce cas

Quantité de lignes par 2 points – Grille (4, 4)
Sur cette grille, on peut former quatre types de triangles rectangles dont a visualisé l'hypoténuse. Ce sont les quatre seules pentes possibles. Se reporter à la page: quantité de triangles rectangles pour l'exposé de la formule utilisée ci-dessous.
Bleu Q(4411) = (4 – 1) (4 – 1) = 3 x 3 = 9 P(4411) = (4 – 2x1) (4 – 2x2) = 2 x 2 = 4 O(4411) = 9 – 4 = 5 Total: 2 x 5 = 10 avec obliques dans l'autre sens.
Rouge Q(4421) = (4 – 2) (4 – 1) = 2 x 3 = 6 P(4421) = (4 – 2x2) (4 – 2x2) = 0 O(4421) = 6 Total: 4 x 6 = 24 avec obliques dans les trois autres sens.
Noir Q(4431) = (4 – 3) (4 – 1) = 1 x 3 = 3 P(4431) = (4 – 2x3) (4 – 2x2) = / O(4431) = 3 Total: 4 x 3 = 12 avec obliques dans les trois autres sens.
Vert Q(4432) = (4 – 3) (4 – 2) = 1 x 2 = 2 P(4432) = (4 – 2x3) (4 – 2x2) = / O(4432) = 2 Total: 4 x 2 = 8 avec obliques dans les trois autres sens.
Total grille 4 x4 Avec les 2x4 droites horizontales et verticales: 8 + 10 + 24 + 12 + 8 = 62 Sur une grille 4x4, on peut tracer 62 droites qui passent par deux points ou plus. Formule Se reporte au calcul pas à pas. Une expression encapsulant toute cette procédure existe, mais pas simple. Voir les Références

Quantité de droites passant par deux points
2 points exactement	0, 0, 6, 12, 48, 108, 248, 428, 764, 1196, 1900, 2668, 3824, 5244, 7248, 9380, 12192, 15372, 19528, 24020, 29732, 36052, 43808, 51836, 61636, 72492, 85308, 98492, 114012, 130668, 150196, 170828, 194768, 220276, 249452, 279284, 312572, 348036, …
2 points ou plus	0, 0, 6, 20, 62, 140, 306, 536, 938, 1492, 2306, 3296, 4722, 6460, 8830, 11568, 14946, 18900, 23926, 29544, 36510, 44388, 53586, 63648, 75674, 88948, 104374, 121032, 139966, 160636, 184466, 209944, 239050, 270588, 305478, 342480, 383370, 427020, …

DicoNombre 48 / 62

Suite	Quantité de droites par trois points Quantité de carrés dans le quadrillage d'un rectangle Constructions élémentaires: rectangle Le terrain de basket Losange Pavage avec des rectangles Quadrilatères – Juniors
Voir	Allumettes en carrés Allumettes et quadrillage Carré Construction à la règle et au compas Dénombrer – Index DicoMot Maths Énigmes classiques Ensembles – les compter Géométrie Pentominos Jeux – Index
Sites	A018809 – Number of lines through exactly 2 points of an n X n grid of points A018808 - Number of lines through at least 2 points of an n X n grid of points On lines and their intersection points in a rectangular grid of points – Seppo Mustonen – Référence sur ce sujet qui note quelques erreurs sur les pages indiquées ci-dessus. On lines through a given number of points in a rectangular grid of points – Seppo Mustonen Some formulas for numbers of line segments and lines in a rectangular grid - Pentti Haukkanen and Jorma K. Merikoski - Niveau supérieur.
Cette page	http://villemin.gerard.free.fr/GeomLAV/Carre/SegGril2.htm