|
|||||||||||||||||||||||||||||||||||
Voir Propriétés fondamentales
des triangles
![]()
|
Droite d'Euler En géométrie, cette droite fut nommée en l'honneur de Leonard Euler (1707-1783) son découvreur
(1763). Cette droite d'Euler passe par
une multitude de points remarquables de tout triangle, sauf le triangle
équilatéral. Elle fut découverte comme la droite portant le centre de
gravité, l'orthocentre et le centre du cercle circonscrit au triangle. Euler explique sa découverte dans: une solution simple à un problème
difficile. Il était alors à Berlin, travaillant pour le compte de Frédéric le
Grand. |
Anglais:
Euler
line /
|
|
|
|
Dans tout triangle, l'orthocentre, le centre de gravité
et le centre du cercle circonscrit appartiennent à une même droite, la droite
d'Euler. Si le triangle est équilatéral
les trois points sont confondus. De plus: HG = 2 GO. Cette droite passe également par le centre
du cercle de neuf points. Elle passe également par le point Exeter. D'autres points existent, les uns plus
sophistiqués que les autres (Voir
site ETC). English
corner Leonhard Euler noticed that three of the many centers of a triangle
are always collinear. This line has come to be named after him - the Euler
line. The three centers that have this property are the triangle's centroid,
circumcenter and orthocenter. Voir Anglais |
|
Voir Droite d'Euler
et construction du triangle (AGH)
|
|
||
|
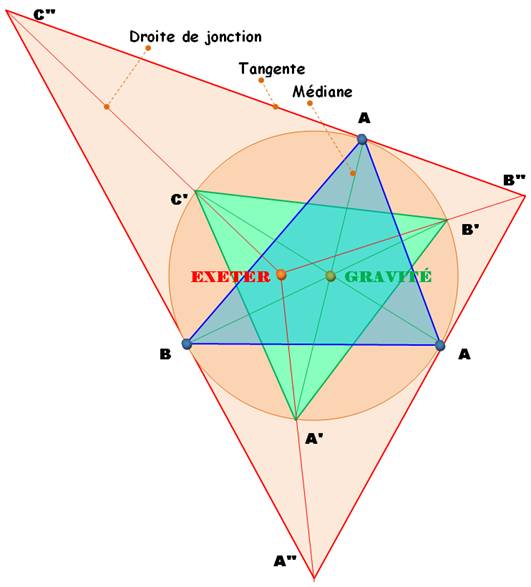
Un triangle ABC
(bleu). Son cercle circonscrit. Les médianes
coupent ce cercle et forment le triangle A'B'C' (vert). Les tangentes au
cercle passant par les sommets forment le triangle A"B"C"
(rose). Les droites (de
jonction) A'A", B'B" et C"C' sont concourantes en E, le point Exeter. Ce nom vient du fait que ce point a été découvert au Philips Exeter
Academy en 1986. |
|
|
Voir Points remarquables du triangle
|
|
|
|
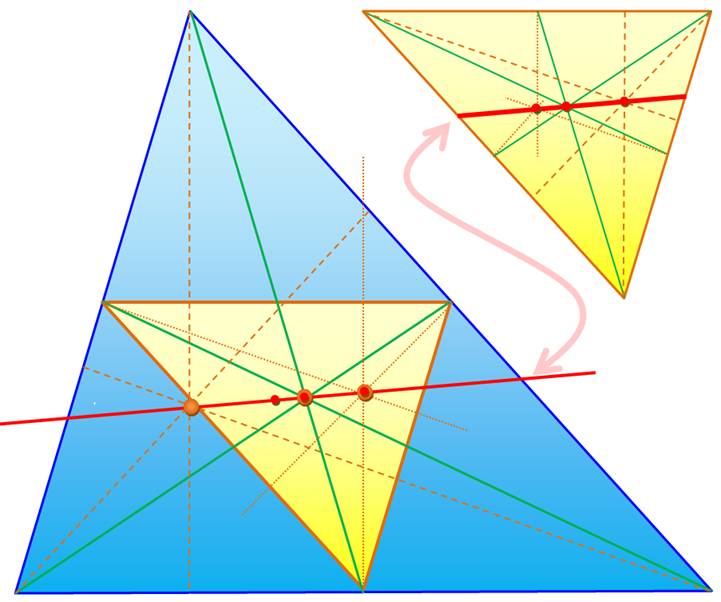
Le triangle médian d'un triangle est le
triangle dont les sommets sont les milieux des côtés. Sur cette figure le triangle de
départ (bleu) et son triangle pédal (jaune), lequel est répété en haut à
droite. Sur chacun, on construit la droite
d'Euler (rouge).
Les deux droites d'Euler sont
confondues. Le point de concours des médiatrices
du triangle est confondu avec le point de concours des hauteurs du triangle pédal
(point rouge de droite). Le point de concours des médianes du
triangle est confondu avec le point de concours des médianes du triangle
pédal (point rouge du centre). Les troisièmes points de la droite
d'Euler sont généralement distincts. Ce qui engendre un nouveau point sur
la droite d'Euler: le point de concours des médiatrices du triangle pédal, le
centre du cercle circonscrit au triangle pédal. |
|
|
|
||
|
En 1763, Euler explique sa découverte dans: une
solution simple à un problème difficile (Solutio facilis problematum quorumdam
geometricorum difficillimorum). Il était alors à Berlin, travaillant pour le compte de Frédéric le
Grand. C'est en 1767 qu'il publie son article à
l'Académie de Saint-Pétersbourg du temps de Catherine la Grande. |
Euler commence par récapituler les quatre
points remarquables du triangle: orthocentre, centre de gravité, centre du
cercle circonscrit, centre du cercle inscrit. Il note que si deux point son confondus,
ils le sont tous et le triangle est équilatéral. |
|
|
Il fait état des formules
de Héron pour calculer l'aire du triangle quelconque. |
A²
=1/16 (a+b+c)(a+b-c)(b+c-a)(c+a-b) A²
= 1/16 (2a²b² + 2a²c² +
2b²c² -a4-b4-c4) |
|
|
Il se fixe un système de d'axes et calcule les
coordonnées des points remarquables |
Orthocentre H >>> Centre de gravité G >>> Centre du cercle circonscrit
O >>> Centre du cercle inscrit I >>> |
|
|
La suite comporte de nombreuses pages de calcul
impliquant les solutions d'une équation
cubique. |
z3 - pz² + qz – r = 0 |
|
|
Euler montre que des trois d'entre eux sont
colinéaires. Il donne aussi une relation entre les quatre
points. |
HO
= 3/2 HG 4OI²
+ 2HI² = 3HG² + 6GI² |
|
|
En fait, il poursuit, car son but était la marche
à l'envers: construire un triangle connaissant ces quatre points. |
À
nouveau un calcul complexe! |
|
Pour une explication plus détaillée
voir le site:
How Euler did it
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette
page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/DrEuler.htm
|
![]()