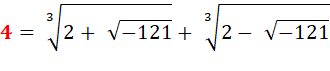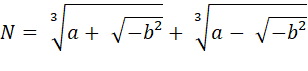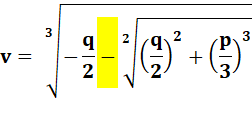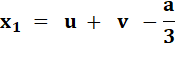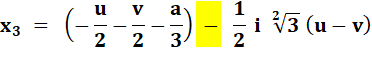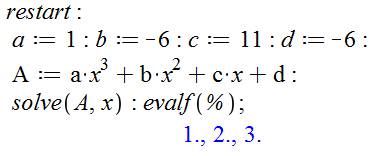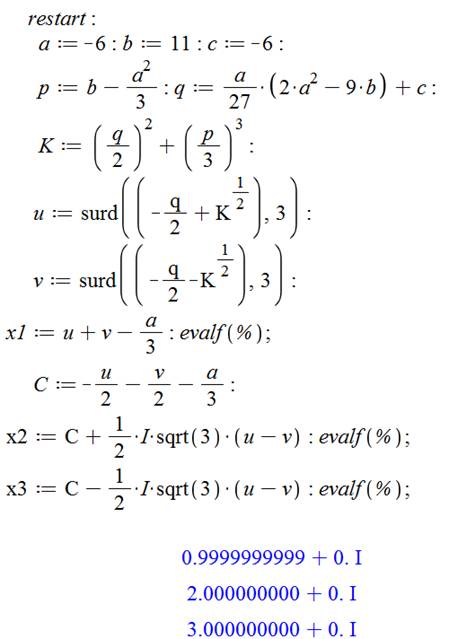NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/07/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ÉQUATIONS
Débutants Équations	Troisième degré				Glossaire Équations
INDEX Équations	Théorie	Exemple 1	Méthode	Historique
	Factorisation	Exemple 2	Exemple 3	Symétrie
	Nombre d'argent			Rac. cub. de a
		Sommaire de cette page >>> Cas de la valeur 4 (Bombelli) >>> RÉSOLUTION >>> Expression complète >>> Forme trigonométrique >>> Programmation directe >>> Programmation de la formule de calcul

Équations du troisième degré

C'est déjà du coriace !!!

Voici un peu de théorie.

Je souhaite voir un exemple tout de suite >>>

Je sais faire rapidement avec une méthode bestiale >>>

Avant de vous lancer dans les calculs longs et fastidieux de résolution des équations du troisième degré, vérifiez qu'il n'y a pas une racine évidente >>>

Avant de me lancer, je voudrais me familiariser avec ce genre d'équations >>>

Cas de la valeur 4 vue par Bombelli
Voici un cas pour se familiariser à la résolution des équations du troisième degré. Des valeurs étranges en racines cubiques de racines carrées de nombres négatifs! Confrontés à ces bestiaux, les mathématiciens des années 1500 ont eu du mérite à trouver les solutions. Ce fut une recherche sur fond de secrets et de coups tordus.
En 1560, Bombelli cherche à résoudre l'équation indiquée.	x^3 = 15 x + 4
Il a l'intuition que la racine doit être de la forme:	2 + a . i (notation moderne avec les complexes).
Cette expression au cube donne.	8 – 6a^2 + i (12a – a^3)
À égaler avec la partie sous radical.	8 – 6a^2 + i (12a – a^3) = 2 + 11 i 8 – 6a^2 + i (12a – a^3) = 2 + 11 i
En égalant séparément la partie réelle et la partie imaginaire.	8 – 6a^2 = 2 12a – a^3 = 11
Ce qui donne:	a = 1
Bilan:	(2 + i)^3 = 2 + 11 i
En replaçant dans la formule initiale:
On vérifie que 4 est bien solution de l'équation étudiée:	4^3 = 15 x 4 + 4 = 64

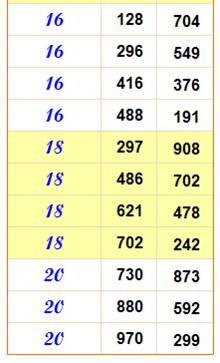
Cette formule en avec N entier est rare. En voici deux autres: Toutes les valeurs pour a et b jusqu'à 1000, b étant un carré
Quelques unes des rares valeurs, b NON-carré

Voir Conjugués complexes / Nombre 4 / Nombre 6 / Nombre 12

Équation du 3^e degré – Formules de résolution
	Trois racines réelles.
	Une solution réelle et deux racines complexes conjuguées.
	Racine simple et racine double.

Voir Exemples pratiques

Expression complète
Attention les coefficients a, b, c et d ne sont pas ceux indiqués ci-dessus. Ici, a est le coefficient de x^3. et non celui de x^2.

Merci à Joseph P. pour sa contribution

Résolution trigonométrique
On pose
L'équation devient
Et les racines	avec k = {1, 2, 3}

Voir Trigonométrie

Programmation directe
Calcul direct avec l'instruction solve NB. "a" est le coefficient de x^3.	To solve en anglais veut dire résoudre. Réinitialisation générale. Définition des coefficients. Définition de l'équation A. Résolution en x de l'équation A. Et, évaluation numérique (flottante) des solutions. Affichage des trois solutions: 1, 2 et 3
Vérification par factorisation (x – 1)(x – 2)(x – 3)	= (x – 1) (x² – 3x – 2x + 6) = (x – 1) (x² – 5x + 6) = x^3 – 5x^2 + 6x – x² + 5x – 6 = x^3 – 6x^2 + 11x – 6
Vérification avec les racines x^3 – 6x^2 + 11x – 6	Pour x = 1 => 1 – 6 + 11 – 6 = 0 Pour x = 2 => 8 – 24 + 22 – 6 = 0 Pour x = 3 => 27 – 54 + 33 – 6 = 0

Voir Résolution avec tableur / Programmation

Programmation de la formule de calcul
	Attention à la définition des coefficients Réinitialisation générale. Définition des coefficients. Calcul des variables intermédiaires p et q. On pose K la somme du carré et du cube. Calcul des variables intermédiaires u et v. L'instruction surd (radical en anglais) calcule la racine énième d'une valeur; ici la racine troisième. Voir Explications Calcul des racines et évaluation numérique. Affichage des trois racines avec la partie réelle et la partie imaginaire nulle.

Suite	Autres exemples du 3^e degré Autres pages sur 3^e degré Résolution symétrique de Lagrange Réduction des termes d'une équation
Voir	Algorithme d'Héron Équation de Pell Méthode de Newton Système d'équations particulier
Sites	Vous introduisez les coefficients et la réponse est immédiate. Solve cubic equation – Wolfram Cubic equation calculator
Cette page	http://villemin.gerard.free.fr/ThNbDemo/Eqa3d.htm