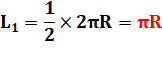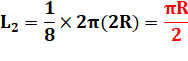|
|||||||||||||||||||||||||||||||||||||||
![]()
|
OVALE – OVE
Voir Ellipse Forme ovale: forme convexe fermée arrondie comme l'ellipse ou l'ove et d'autres. Elle a au moins un axe
de symétrie.
Généralement construit à Ballon ovale: ballon de rugby. Ove: en forme d'œuf.
Ovoïde: ove en trois dimensions, de révolution autour de
l'axe de symétrie. Oblong: rectangle
avec deux demi-cercle aux extrémités. Capsule: forme oblongue de révolution. |
Anglais: oval,
egg curve / obround or stadium or discorectangle pour oblong
|
|
||
|
La construction de l'ove classique telle
qu'elle se trouvait dans les livres de géométrie de nos grands-pères. 1. Un cercle de
diamètre AB = 2R; 2. Deux cercles de centre A et B et de rayon AB qui se coupent en M et N; 3. La droite MN est la médiatrice du segment
AB; 4. Deux demi-droites AC et BC qui coupent les cercles en D et E. 5. Cercle de centre C et de rayon CD (= CE). |
|
|
|
|
|||
|
Aire de l'ove = Aire 1 (demi-cercle
ABF) + Aire 4 (quart de
cercle) + 2 x Aire 3
(secteurs ABD et BAE) – Aire 2 (triangle ABC) Quelques remarques L'angle
ACB inscrit dans un
demi-cercle est droit (Pi/2). Les
segments AC et BC ont même longueur (cf. médiatrice). Le
triangle ABC est isocèle
rectangle. |
L'aire de l'ove (bleue) est proche de celle du grand carré rose (99,5%). |
||
|
Calcul des longueurs |
|
||
|
Aire 1 (aire du disque) |
|
||
|
Aire 2 (demi-carré) |
|
||
|
Aire 3 (aire du secteur) aussi 1/8 de
disque |
|
||
|
Aire 4 (quart de disque) |
|
||
|
Aire de l'ove |
|
||
|
Formules |
|
||
|
|
||
|
Quatre arcs |
AFB,
AB et BE puis DE |
|
|
AFB = demi-cercle |
|
|
|
AB = BE = 1/8 de cercle |
|
|
|
DE = quart de cercle |
|
|
|
Périmètre de l'ove |
|
|
|
Formules |
|
|

|
|
||
|
On
connait la construction du jardinier
pour l'ellipse avec deux piquets. Il suffit
d'en ajouter un troisième pour obtenir l'ove. Les trois piquets formant un triangle isocèle. La
ficelle tendue par le crayon doit être un peu pus longue que le périmètre du
triangle. Les
courbes développées sont des arcs d'ellipses. Pour être
plus exact (lisser les points de connexion), il faudrait construire encore
trois autres ellipses plus grandes. |
|
|
|
|
||
|
Équation
de l'ellipse:
Équation
de la forme ovale:
Illustration En
rouge: ellipse classique: x²+ y²/4 = 1 En bleu: ovale: x²+ (y/(2+0,6x))²
= 1 En vert: ovale: x²+ (y/(2+1,2x))²
= 1 |
|
|
|
Équation
du cercle
Équation
de la forme ovale:
Illustration En
rouge: cercle: K = 1 En bleu: ovale:
K = exp (x ln2) En vert: ovale:
K = exp (x ln3) |
|
|
|
|
||
|
Ovale de
Cassini: lieu des points tels que le produit FM.FM' est constant. Avec
FM.FM' = a² et FF' = 2e, l'équation s'écrit: (x² + y²)² – 2e² (x² – y²) – a4 + e4
= 0 Illustration du bas avec e = 6 et Rouge: a =
8,5 (externe) Bleue: a = 8 Rouge: a = 6 Bleue: a = 4 Allure selon a comparé à e
|
|
|
Voir Lemniscate
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |
![]()