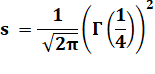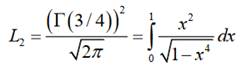|
|||||||||||||||||||||||||||||||||||
![]()
|
Lemniscate Lemniscate de Bernoulli La
lemniscate est une courbe en forme de huit, cas particulier de l'ovale de Cassini.
|
|
Définition Courbe
en forme de huit et qui est le lieu géométrique des points tels que le produit
de leurs distances à deux points fixes est constant. Courbe en 8, symbole de l'infini. Étymologie Du
latin lemniscatus venant du grec lemniscos: rubans attachés aux couronnes,
aux palmes des vainqueurs et des suppliants, ou ornant la tête des convives
dans un festin. Anagramme: LEMNISCATE ó
CENTESIMAL Voir
Anagrammes Ésotérisme (voir la frise
ci-dessus) Le
tarot
XI, la force, porte parfois une auréole en forme de lemniscate. Le
serpent d'Ouroboros
est lové en cercle, parfois représenté en huit. Historique En
1680, Giovani Cassini (1625-1712) étudie les formes ovales qui portent son
nom. Il pensait que le Soleil suivait une orbite de cette forme. La
lemniscate est un cas particulier de ces courbes. En
1694, Jaques (Jakob) Bernoulli
(1654-1705) publia dans Acta Eruditorum une courbe qu’il appela lemniscate.
Son frère Jean (1667-1748, formateur d'Euler) avait découvert cette courbe en
même temps et indépendamment. Ses recherches sur cette courbe l’ont amené à
définir cette courbe dont le calcul de la longueur d’un arc conduit plus tard
à l’introduction des fonctions elliptiques. En
fait, La naissance de la théorie des fonctions
elliptiques remonte à l'examen par Euler (1751) des travaux du compte
Giulo Fagnano (1682-1766) sur
la lemniscate, lequel avait connaissance des travaux des Bernoulli. |
Sources
CNTRL / CNRS –
Images de maths
|
|
||
|
Définition de la lemniscate |
Lieu des points M tels que, par
rapport à deux points F et F' (les foyers), le produit MF . MF' est constant. Gian Malfetti (1731-1807) a démontré
qu'un corps se déplaçant par gravité sur un arc quelconque de lemniscate va
aussi vite qu'un corps qui se déplacerait sur la corde sous-tendue par l'arc. |
|
|
Traduction algébrique Avec le
théorème de Pythagore; voir figure ci-dessous. |
Cette égalité qui est également
valable pour leur carré. MF² . MF'² = (y² + (c – x)²) (y² +
(c + x)²) = c4
= (y2 + c2 – 2cx +x2) (y2
+ c2 – 2cx +x2) = c4
= y4 + 2x2y2 + x4 +2c2y2
– 2c2x2 + c4 = c4
|
|
|
Appréciation |
Pour c = x = 1, alors: y = (y² +
4)y² – 1
|
|
|
Coordonnées cartésiennes
Notez
que: a² = 2c² |
|
|
Calcul en polaire Avec la forme
polaire:
|
Voir Identités
trigonométriques
|
|
Coordonnées polaires
|
|
|
|
||
|
|
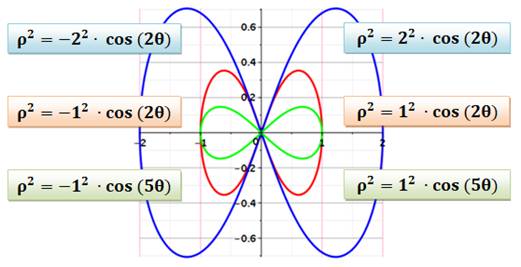
Description polaire et graphique
cartésien Réinitialisation générale (start). Commande de dessin de courbe (plot) Description de la courbe pour x positif (tracé rouge)
et pour x négatif (tracé bleu). Angle 2t variant de -90° à 90°. Notez que pour
les autres valeurs le cosinus est négatif et il est impossible de prendre sa
racine carrée. Maple admet toutes sortes de types de
coordonnées, dont les coordonnés polaires. Définition de la couleur de la courbe, de son
épaisseur et de la police (font) des
nombres sur les axes. Dessin de la lemniscate. Pour obtenir la même échelle sur les deux axes,
sélectionner la courbe et dans le menu qui s'affiche, cliquer sur 1:1. |
|
|
|
Description polaire et graphique
polaire Ci-dessus la définition était exprimée en
coordonnées polaire et le graphe réalisé en coordonnées cartésiennes. Ci-contre, le graphe est représenté en
coordonnées polaires. Cette fois, il faut appeler les logiciels de dessin (plots). |
|
|
|
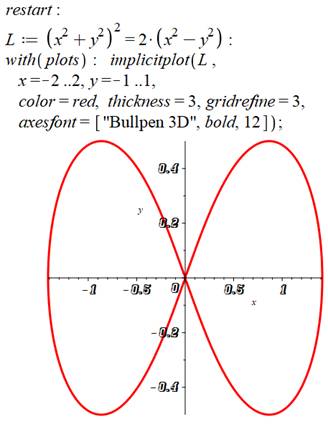
Description cartésienne et
graphique cartésien L'équation (L) de lemniscate est indiquée en x et
en y Les logiciels de dessin sont appelés Dans la mesure où x et y sont présents, c'est le
dessin implicite (implicitplot) qui est
spécifié. L'amplitude de la représentation en x comme en y
doivent être spécifiés. Une nouvelle instruction fait son apparition: gridrefine (affiner la grille). Elle détermine
la résolution du calcul. Avec 1, on
verrait apparaitre une ligne brisée et un trou vers x = 0. La fonte sur les axes est l'une de toutes celles
dont vous disposez sur votre ordinateur.
|
|
Voir Programmation – Index
|
|
|||
|
Pas facile! Transcendant La
longueur d'un arc de lemniscate, comme celle de l'hyperbole ou celle de
l'ellipse, se calcule avec une intégrale transcendante. Autrement-dit; aucune formule élémentaire ne permet de la
calculer. Il existe bien l'égalité de Fagnano => Elle est à l'origine des calculs par intégrale. |
Fagnano découvre cette étonnante
relation
Relation qui dit qu'un arc de lemniscate = arc d'ellipse
+ arc d'hyperbole. Avec
Suite
sur le site de
Jean-Claude Pénin |
||
|
Une idée de cette longueur Quel est l'ordre de grandeur du rapport entre le périmètre (L) et la
longueur (c), constante de la lemniscate ? Total des mesures: Rapport L/c: 26,12 x 4 / 20 = 5,23 |
Approximation par des segments
d'une aile de la courbe
|
||
|
|
|||
|
La constante s est le périmètre de la lemniscate pour c
= 1. Son calcul fait intervenir la fonction
gamma. Elle joue un rôle semblable à celui de Pi
pour le cercle. En 2016, elle est connue avec 250 milliards de
décimales - Ron Watkins |
= 0,39894 … x 3,62561…2 |
||
|
Exemple
|
c = 1 et a = 0,707 Hauteur totale: 0,707 … Longueur totale: 2 Périmètre complet: 5,244… Aire: 1 |
||
|
Constante L1 et L2 La première constante
représente la longueur d'un quart de lemniscate La deuxième constante est égale à la moitié de la
constante
de Gauss. |
L1 = 1,311028777… L2 = 1 / 2G = 0,5990701173 … G = 0,834626841167 … |
||
|
Calcul des constantes |
|
||
|
Identité d'Euler (1781) |
|
||
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()