|
Édition du: 07/10/2024 |
|
INDEX |
Histoire des maths – Antiquité |
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
QUADRATURE DU CERCLE Exemples de constructions Les
Anciens ont cherché à dessiner à la règle et au
compas un carré
qui aurait la même aire que le cercle
(disque). Ils n'arrivaient qu'à des solutions approchées sans trouver la
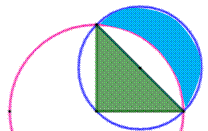
bonne. En 1882, L'aire de
la lunule
(ou lune) d'Hippocrate est rigoureusement égale à celle d'un triangle
(bleu = vert). Une telle propriété a longtemps fait penser que la quadrature
du cercle était réalisable. En 2019,
Hung Viet Chu donne une construction correcte à neuf décimales.
|
||
|
|
Sommaire de cette page >>> Construction pratique des Égyptiens >>> Constat d'Archimède >>> Construction pratique du jardinier >>> Construction simple >>> Pi
approché par Hobbes >>> Pi approché avec roulement >>> Construction de Kochanski >>> Construction de Jacob de Gelder >>> Construction d'Hobson >>> Construction de Dickson |
Débutants Glossaire |
Anglais: it is
impossible to square the circle by compass and straightedge
|
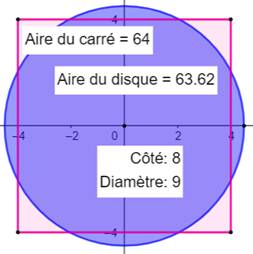
Construction Cercle de
diamètre 9 et Carré de côté 8. Aires Carré: 8 × 8 = 64 Disque: π × 4,5² = 63,6172… Écart: 0,6% Calcul
de p = Pi approximé
|
|
|
|
Construction Cercle de rayon
unité. Triangle
rectangle (R, P) avec R le rayon du cercle et P son périmètre. Aires Disque : π
R² Triangle: ½ P ·
R = π R² Archimède
constate cette égalité des aires dans son traité: De la mesure du cercle. |
Pour rectifier
le cercle en un triangle rectangle, il "suffit" de savoir tracer la
longueur du périmètre du cercle (autrement-dit, une longueur Pi). |
|
|
Méthode Utilisation
d'une corde et d'un piquet. Construction Dessiner le
cercle bleu façon jardinier. Avec la corde enroulée
sur le demi-cercle reporter cette longueur en DG. Avec la corde de
longueur GB, la plier en deux pour trouver K, le milieu de GB. Cercle (K, AB). Perpendiculaire
DF; intersection en H. HD est le côté
du carré. |
|
|
|
Une construction
simple, sans respecter la contrainte règle et compas (semblable à la
précédente). Construction Cercle de
rayon OA = 1. Prolonger OA tel
que AB = Pi . Milieu O' de AB. Cercle (O',
O'O). Perpendiculaire
AC en A à AB. Carré de côté
AC. Alors l'aire du
disque vaut Pi et celle du carré également. |
|
|||||||||||
|
Calculs
|
||||||||||||
Voir Brève
858
|
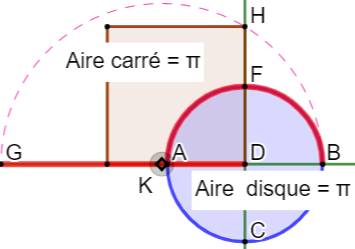
Quadrature de Pi Un cercle de centre C et
de rayon unité roule sans glissement d'un demi tour et progresse d'une
longueur AB égale à Pi. Il se retrouve ne position D. Le demi-cercle bleu à pour diamètre AF, la somme de ces segments (Pi + 1). La perpendiculaire DH à partir du centre du cercle en position finale D coupe le cercle bleu en H. Le segment BH est la hauteur du triangle rectangle AHF. Sa longueur est connue : BH² = AB . BF = Pi x 1 = Pi Le carré de côté BH a une aire égale à Pi. |
Comment tracer un segment de longueur racine de Pi
|
|
Cité par Hervé Lehning
|
Construction de Thomas Hobbes (1588-1679)
Conclusion
Calculs
|
Figure
Cercle et triangle:
périmètres voisins Comparaison
Note Ramanujan
a aussi retrouvé cette approximation de |
|||||||||||||||||
|
Principe Approximation de
Pi avec quatre décimales correctes par:
Une prouesse pour l'époque. Construction
de "Pi" Cercle unité en
bleu. Diamètre
orthogonaux: BD, CE. Tangente en E Cercle (D, 1);
intersections F et G. Cercles (G, 1),
(H, 1) et (I, 1): intersection J. La longueur de
CJ est proche de Pi. |
|
||
|
Calculs
|
|||
|
Construction
du carré Perpendiculaires
en C et J à CJ. Cercle (J, 1) et
(L, 1). Intersections L
et K. Demi-cercle LK. Perpendiculaire
en M à KL. Intersection N. LN est le côté
du carré. |
|
||
Voir Construction de Kochanski – Autre
présentation
|
Principe Approximation de
Pi avec six décimales correctes par:
Construction
de "Pi" Cercle bleu de rayon unité. CE = 7/8 Segment AE. AF = 1/2 FG // CD et
FH // EG AJ = 3 JK = AH
Construction
du carré Demi-cercle AK, intersection M BM est le côté
du carré. |
|
|
|
Calculs
|
||
|
Principe Approximation de
Pi avec trois décimales correctes par:
Avantage d'une extrême simplicité. Construction
du carré Cercle bleu de
rayon unité OD = 3/5, OE = 1/2
et OF = 3/2 Demi-cercle (DE)
et (AF) Intersections G
et H GH est le côté
du carré. |
|
|
|
Calculs
|
||
|
Principe Approximation de
Pi avec trois décimales correctes par:
Construction AB = 1 AD = 1
perpendiculaire à AB. Cercle (A, AB),
le cercle de référence. C le milieu de
AD. Cercle (C, CB),
intersection E. Cercle (D, DE),
intersection F. FH = 1 GF = 3/10 de AF. Cercle de
diamètre HG. FI
perpendiculaire à GH. IK = FI; FK est le côté du carré. |
|
|
|
Calculs
Hùng Viêt Chu propose une simplification de cette
méthode et décrit une méthode produisant 9 décimales correctes. |
||
![]()
|
Retour |
|
|
|
Suite |
Voir Quadrature du carré
|
|
|
Voir |
|
|
|
|
||
|
Cette page |
||