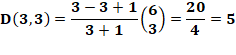|
Édition du: 04/04/2023 |
|
INDEX |
Types de Nombres – GRILLES |
||
Faites un double-clic pour un retour en haut de page
![]()
|
CHEMINS de DYCK Mots de Dyck Chemin dessiné
sur une grille (anglais: lattice path). Déplacement vers
la droite ou vers le haut seulement. Par nature, ces chemins sont
naturellement auto-évitants. |
||
|
|
Sommaire de cette page >>> Chemins de Dyck >>> Mots de Dyck |
Débutants Glossaire |
|
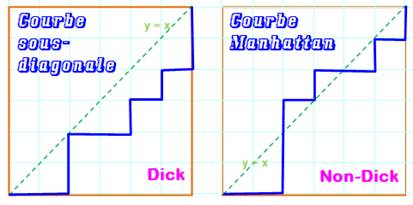
Mouvements contraints en dessous de
la barre oblique Un chemin de Dick est un chemin en escalier (pas vers le nord ou vers l'est). Le chemin est sous-diagonale:
il est contenu dans le triangle bas-droite. Le chemin peut aller jusqu'à la
diagonale, mais sans jamais la dépasser. |
|
|
|
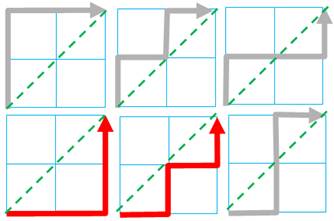
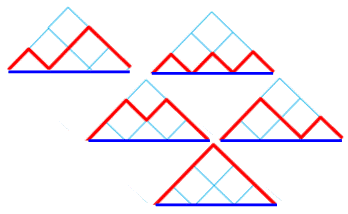
Exemples La figure du haut montre les "rescapés"
pour une grille 2 × 2. Il en reste seulement deux dont le chemin ne fait pas une
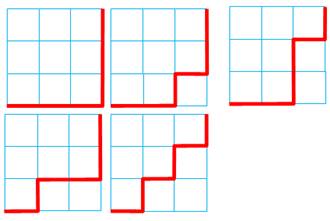
incursion au-dessus de la diagonale verte. Q(2) = 2 En bas, les "rescapés" pour une grille
3 × 3. Il en reste
seulement cinq. Q(3) = 5 Formule de Delannoy Quantité de chemins de longueur n pour rejoindre
l'altitude k:
Exemple
Codage binaire de ces chemins Un pas vers la droite est codé par un
"1" et par un "0" pour la montée. On aura les codes suivants (dans l'ordre de la
figure): 111000; 110100;
110010; 101100; 101010 |
Grille 2 × 2: deux chemins
Grille 3 × 3: cinq chemins
Représentation sous la forme de
montagnes
|
|
Les 14 chemin de Dick de
longueur 8
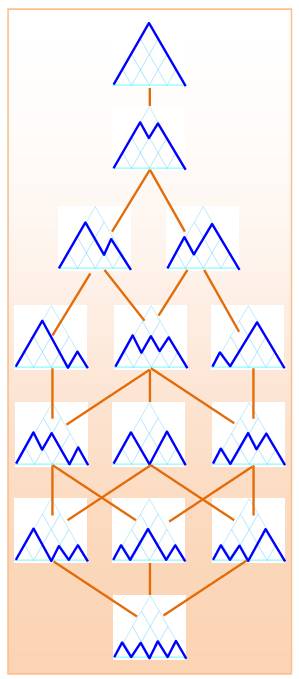
Vocabulaire des chemins de Dyck

|
Les pas (steps) sont
notés U (up) pour un mouvement montant (1, 1) et D (down) pour un mouvement
montant (1, –1). La suite des U et D, parfois transformée en suite de 1 et 0
est appelée mot de Dyck. Deux
présentations possibles: droite ou oblique. Sa longueur est 2n et son
altitude maximum est n. Intérêt Les chemins de
Dyck font l'objet de très nombreuses études par les mathématiciens. Notations
et vocabulaire précis s'imposent pour "mathématiser" les recherches
sur ce sujet. Alors, les
développements deviennent vite affaire d'experts de niveau universitaire. Voir Articles d'Emeric Deutsch et
celui de François Bergeron. La plupart des
recherches consistent à énumérer les chemins de Dyck selon plusieurs paramètres,
tels que la longueur, nombre de sommets (ou pics) ou de vallées, nombre de
doubles montées, nombre de retours à l'axe des abscisses. D'autres études
examinent les classes de chemins de Dyck contraints, évitant certains motifs
ou ayant une structure spécifique. La quantité de
chemins de Dyck comportant exactement à k sommets est égale aux nombres de Narayana. |
Anglais
|
Présentation
oblique A Dyck path is a
staircase walk from (0, 0) to (n, n) lying below the diagonal (y = x). Présentation
droite A Dyckpath is a path in
the first quadrant which begins at the origin, ends at (2n, 0), and consists
of steps (1, 1) (North-East), called rises, and (1, – 1) (South-East), called
falls. We shall refer to n as the
semilength of the path. Occasionally, a Dyck path of semilength n will be called a Dyck n-path. |
|
Mot de Dyck |
Chaine de caractères (mot) comportant seulement
les lettres X et Y, tels que dans chaque préfixe du mot on a: Arrangement correct de k paires de parenthèses
(pas plus de fermantes que d'ouvrantes déjà écrites). Codage binaire avec moins de 0 que de 1 déjà
écrits à gauche du mot binaire. Chemins de Dyck: la
contrainte se traduit par le fait que le chemin est toujours au dessus de
l'axe des x. Un mot de Dyck est un mot M tel que M possède
autant de fois chaque lettre, et tel que tout préfixe de M ne contienne pas
plus de fois la lettre X que la lettre Y. Par exemple, le mot XXYY est un mot
de Dyck, alors que XYYX n’en n’est pas un. On peut remplacer les X et Y par des parenthèses:
(()(()())) est vade mais pas ()())(. Le motif doit respecter des paires de
parenthèses équilibrées (une parenthèse ouvrante doit retrouver un compagnon
fermant). La quantité de mots de Dyck de longueur 2n est Cn. Le nombre d'arbres binaires à n + 1 nœuds vaut Cn. Le nombre de façons de calculer un produit
associatif de n + 1 termes est Cn. Le nombre d'arbres binaires à n + 1 nœuds vaut Cn. |
|||
|
Exemple avec longueur 2 Exemple avec longueur 6 Lettres, binaire et parenthèses |
XY, XX 10, 11 XXXYYY,
XYXXYY, XYXYXY, XXYYXY,
XXYXYY 111000,
101100, 101010, 110010, 110100 ( ( ( ) ) ), ( ) ( ( ) ), ( ) ( ) ( ), ( ( ) ) ( ), ( ( ) ( ) ) |
|||
|
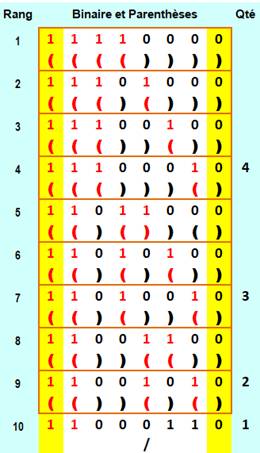
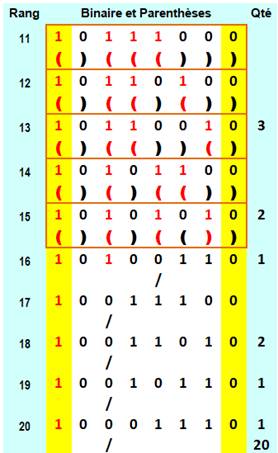
Correspondance avec les parenthèses Quantité égale de parenthèses ouvrantes et fermantes; mais pas plus de
fermantes que d'ouvrantes déjà positionnées. Les lignes 10 et 16 à 20 sont ainsi éliminées. Codage binaire: 1 ouvrantes (en
rouge) et 0 pour fermantes (en noir). Avec quatre jeux de parenthèses, il y a: 14 motifs. C'est le quatrième nombre de Catalan. C4 =
14 |
Exemples de longueur 8
Il y a 20 codes binaires comportant quatre
"1" et quatre "0". Seulement 14 sont
valides au sens des mots de Dyck, car comportant moins de
"0" que de "1" en partant de la gauche. Le cas des parenthèses qui ne peuvent pas être
fermées si pas ouvertes fait bien comprendre cette contrainte. |
|||
Voir Parenthèses bien
ordonnées
|
Variétés de
chemin de Dyck (n = 3) Tous dénombrés avec les nombres de
Catalan |
||
|
Chemins de (0, 0) à (n, n) avec pas de (0,
1) ou (1, 0) sans jamais dépasser la diagonale y = x |
|
|
|
Chemins de Dyck de (0, 0) à (2n, 0) avec pas de (1,
1) ou (1, -1) sans jamais passer en dessous de l'axe des x |
|
|
|
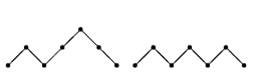
Chemins de Dyck de (0, 0) à (2n+2, 0) tels que la
longueur des descentes soit impaire |
|
|
|
Chemins de Dyck de (0, 0) à (2n+2, 0) sans sommets de
hauteur 2 |
|
|
Source images:
Stanley
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
|
Voir |
|
|
|
|
||
|
Cette page |
||