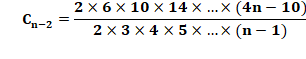|
Édition du: 28/03/2023 |
|
INDEX |
Dénombrement – Suites de nombres |
||
Faites un double-clic pour un retour en haut de page
![]()
|
SUITES pour dénombrer Liste des principales suites et
applications Revue des
principales suites de nombres qui servent à dénombrer des objets: polygones triangulés
ou décomposés, parenthèses, chemins divers sur une grille, cordes dans le
cercle … La page DÉNOMBREMENT
donne accès à toutes les pages relatives au comptage d'objets figurant sur ce
site. |
||
|
|
Sommaire de cette page >>> Suites principales pour dénombrer >>> Historique des principales suites pour compter
>>> Anglais |
Débutants Glossaire |
|
Pascal (triangle) |
1; 1,
1; 1, 2, 1; 1, 3, 3, 1; 1, 4, 6, 4, 1; … Coefficients du binôme. Développement d'un binôme à la puissance k. Combinaison de n objets pris k par k. |
|
|
Narayana (triangle) |
1; 1,
1; 1, 3, 1; 1, 6, 6, 1; 1, 10, 20, 10, 1; … Arbres à n branches et k feuilles. Parenthèses avec k paires internes. Chemins obliques comportant k sommets. |
|
|
Catalan |
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, … Triangulation d'un polygone à 2n côtés en
dessinant des diagonales. Quantité de partitions non-croisées dont chaque bloc Places de n paires de parenthèses dans un mot de
n+1 lettres. Quantité de chemins en escalier contenus sous la
diagonale d'une grille carré. |
|
|
Manhattan |
1, 2, 6, 20, 0, 252, 924, 3432, … Nombres centraux du triangle de Pascal Chemins dans une grille selon progression nord ou
est. |
|
|
Dyck |
Nombres de Catalan. Chemins de Manhattan sans dépasser la diagonale. |
|
|
Bell |
1, 1, 2, 5, 15, 52, 203, 877, 4140 … Partitions d'un ensemble de n éléments. |
|
|
Motzkin |
1, 1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798,
… Chemins obliques sur grille pour parcourir la distance
horizontale de longueur n. |
|
|
Delannoy – Matrice |
1; 1,
3, 5…; 1, 5, 13, 25, 41; 1, 7, 25, 63, 129 …; etc. Chemin sur grille avec progression nord, est et nord-est
: chemin de (0, 0) à (n, k) avec pas (0,1), (1,1) ou (1, 0). Pavages avec dominos particuliers. |
|
|
Delannoy – Nombres |
1, 3, 13, 63, 321, 1683, 8989, 48639, … |
|
|
Schröder |
1, 2, 6, 22, 90, 394, 1806, 8558, 41586, … Chemins dans les mailles d'une grille
en progressant vers le nord, l'est ou le nord-est. |
|
|
Schröder-Hipparque |
1, 1, 3, 11, 45, 197, 903, 4279, 20793, … Arbres plans avec n feuilles. Parenthèses insérées dans
une suite d'éléments. Façon de partager un polygone convexe en
polygones plus petits en dessinant des diagonales. |
>>> |
|
Octaédriques |
0, 1, 6, 19, 44, 85, 146, 231, 344, 489, 670,
891, 1156, 1469, 1834, 2255, … Empilement de deux pyramides successives à base
carrée. |
|
|
Octaédriques centrés |
1, 7, 25, 63, 129, 231, 377, 575, 833, 1159,
1561, 2047, 2625, 3303, 4089, … Chemins dans les mailles d'une grille
en progressant vers le nord, l'est ou le nord-est. |
|
|
Ming Antu (v.1692-v.1763) |
Les nombres de Catalan étaient connus par ces
mathématiciens chinois. En 1730, Ming Antu, mathématicien de Mongolie,
publie: Méthodes rapides pour compter précisément les cordes des cercles. On
y trouve notamment l'utilisation des nombres de Catalan
pour développer les sinus(2a) et sinus(4a) en fonction de sinus(a). |
|||
|
Chen Jixin - 1774 |
C'est en
1988 que le livre écrit par Ming Antu en 1730 et achevé par son élève Chen
Jixin en 1774 est révélé dans une revue chinoise. En 1999, P. J. Larcombe montre que Ming Antu
utilisait les nombres de Catalan pour développer les sinus multiples. |
|||
|
Fibonacci (v.1170-v.1250) |
En 1202, les nombres de
Fibonacci sont décrits dans le livre Liber abaci. |
|||
|
Leonhard Euler - 1760
|
Euler découvre les
nombres de Catalan en répondant à question suivante: combien de façons de découper un polygone convexe en triangles en
dessinant des diagonales qui ne se coupent pas ? Il les compte à la main
jusqu'à C8 = 1430, un exploit ! Après les travaux de Segner, il
calcule jusqu'à C22. Trouve la formule pour les dénombrer en disant
que la formulation de la récurrence est difficile. Par lettres, il questionne Christian Golbach en
1751 puis Segner en 1758, lequel trouve la réponse. |
|||
|
Nicolas Fuss (1755-1826)
|
Connu pour être l'assistant d'Euler de 1772 à
1783 (marié à la fille d'Euler). Nombres de Fuss-Catalan: une
généralisation des nombres de Catalan. En 1793, Johann Pfaff interroge Fuss: sait-on
dénombrer la décomposition d'un polygone en polygones plus petits ? Un mois
plus tard, Fuss publiait un papier sur ce sujet introduisant les nombres e
Fuss. De nombreux mathématiciens ont apporté leurs
contributions: Liouville, Cayley, et en 1998 Jozef Przytycki et Adam Sikora. |
|||
|
Johann Andreas von Segner
(1704-1777)
|
Mathématicien hongrois, il découvre les nombres
de Catalan simultanément avec Euler(1758), lui aussi en comptant les
triangles découpés dans le polygone convexe. Trouve la formule récurrente: |
|||
|
Gabriel Lamé (1795-1870) |
En 1838, publie la preuve complète concernant la
triangulation des polygones (first
self-contained, complet proof). |
|||
|
Olry Terquem, Joseph Liouville,
Olinde Rodrigues, Gabriel Lamé, Eugène Catalan, Jacques Binet, Johanna Grunert, Thomas Kirkman et Édouard
Lucas |
Travaux sur les nombres de Catalan. |
|||
|
Thomas Kirkman |
Redécouvre la formule du nombre de triangulation
du polygone. En fait: k diagonales non concourantes dans un polygone convexe. |
|||
|
Eugène Catalan
|
Catalan était un étudiant de Liouville à
Polytechnique, lequel s'interrogeait sur les travaux d'Euler-Golbach et
Segner. En 1838, Catalan résout ce nouveau problème: étant
donné une suite fixe de lettres, on veut ajouter n – 1 paires de parenthèses de
façon qu'entre chaque couple de parenthèses gauche et droite il y ait deux
lettres. Il relie de résultat à la
triangulation. Sa formule
(conjecture):
Il observe que:
L'idée lui vient après exploration du casse-tête
de la tour
de Hanoï. Il appelait ces entiers, les nombres de Segner.
L'appellation nombres de
Catalan a été donnée en 1948 par John Riordan (1903-1988). En 1878, il publie Sur les nombres de Segner qui traite de la divisibilité des
nombres de Catalan. Plusieurs centaines de publications ont depuis
lors été consacrées aux nombres de Catalan. |
|
Arthur Cayley (1821-1895)
|
Mathématicien clé qui a interprété les nombres de
Catalan en utilisant la notion d'arbre binaire. En 1857, prouve que les nombres de Catalan
représentent la quantité d'arbres dans le
plan avec troncs et à trois feuilles. Publication en 1859. Sa formule:
|
|
William Whitworth (1840-1905) |
En 1878, il introduit le problème du vote. Il le résout et trouve des
applications en combinatoire. Ce problème sera repris par Joseph Bertrand
(1822-1900) qi le redécouvre en 1887 et, ce qui constitue un des premiers
résultat en théorie des probabilités. |
|
Désiré André (1840-1917) |
Trouve une méthode pour compter les chemins de
Dyck (1887). Donne la solution du problème
du vote (ballot problem). |
|
Delannoy (1833-1915 |
Nombres de Delannoy. |
|
Schröder (1841-1902) |
|
|
Édouard Lucas (1842-1891) |
Cite les nombres d Catalan dans son ouvrage: Théorie des Nombres qui, en fait, fait
une part belle à la combinatoire. |
|
Walter Dyck (1856-1934)
|
Étudie les chemins de Dyck,
chemin en escalier en dessous de la diagonale. Exemple
|
|
Eugen Netto (1848-1919) |
En 1901, première introduction classique à la combinatoire. |
|
Motzkin (1908-1970) |
|
|
L. Collatz
(1910-1990) U.
Sinogowitz |
Collatz publie la Théorie spectrale des graphes
(1957): étude des valeurs propres des matrices représentant un graphe.
Application en chimie quantique. Collatz nomme Sinogowitz comme co-auteur, lequel
sera victime du bombardement de Darmstadt en 1944. |
|
Dov Tamari (1911-2006) |
Experte en logique mathématique et combinatoire. |
|
Narayana (1930-1987) |
|
|
H. G. Forder – 1961 |
Établit une relation biunivoque entre la triangulation des polygones et les expressions avec parenthèses. |
|
William Brown – 1965 |
Travail de synthèse sur les nombre de Catalan-
Segner-Fuss. |
|
Henry W. Gould – 1971 (né en 1928) |
Publie: Bibliography of
Bell and Catalan Numbers Décrit 243 cas d'utilisation des nombres de
Catalan. Il en publie 450 en 1976 et énonce 465
références. |
|
Kreweras et Poupard |
Ils étudient les partitions non-croisées et
les nombres de Narayana. Revue historique de ces suites. |
|
Richard P.
Stanley
|
En 1986 et en 1999, il publie
Enumerative Combinatorics. Il demande notamment au lecteur de prouver
l'équivalence de 66 définitions des nombres de Catalan. En 2015, il publie: Catalan
Numbers. Il déclare: Je dois dire que ma séquence de nombres préférée est celle des nombres
de Catalan. [..] Ils sont omniprésents. On savait avant moi qu'il y avait de nombreuses interprétations
combinatoires différentes. [..] Quand j'ai commencé à enseigner la combinatoire énumérative, j'ai bien
sûr abordé les nombres de Catalan. Alors, j'ai commencé par proposer des
interprétations très basiques - n'importe quel cours de combinatoire en
aurait quelques unes - J'aimais en trouver de plus en plus et j'ai décidé
d'être méthodique. Au début, c'était juste une liste dactylographiée. Quand j'ai écrit le
livre, j'ai jeté tout ce que je savais dans le livre. Puis, j'ai continué à
partir de là avec un site web, ajoutant de plus en plus de problèmes. |
Voir Chronologie des
mathématiciens
|
Lattice path: chemin passant par les points d'une grille. Les
coordonnées successives des points définissent une suite de vecteurs, de couples
de nombres. Before to tackle the question of Delannoy numbers and
Delannoy lattice paths, note that the classical number sequences or lattice paths have the name of a mathematician:
It is quite amusing that
some of them are nowadays more famous in combinatorics for problems which can
be explained in terms of lattice paths than in their original field. Delannoy is another
famous name which is associated to an integer sequence related to lattice
paths enumeration. Delannoy’s numbers indeed correspond to the sequence Source: Why Delannoy Numbers ?
Cyril Banderier and Sylviane Schwer |
Voir
Anglais indispensable pour le bac et pour les
affaires
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
||