Ensemble quotient, approche

Édition du: 13/05/2022

INDEX Structures algébriques Théorie des nombres Types de nombres	Structures algébriques
	Débutant	Loi de composition		Table de Cayley
	Relation binaire, équivalence			Groupe
	Classes de congruence		Ensemble quotient
	N = 1 mod k (k = 2, 3,…)		Groupe cyclique

Faites un double-clic pour un retour en haut de page

ENSEMBLE QUOTIENT

Mot mystérieux qui, abordé trop rapidement, peut dérouter, alors qu'il s'agit d'une notion des plus simples à comprendre.

Cette notation indique simplement que l'on considère l'ensemble des nombres de 0 à k et on le note Z_k.

Ces nombres sont tout simplement les restes possibles de la division par k. En fait, l'ensemble quotient oublie les quotients et ne garde que les restes de la division !

Il s'agit donc d'un système de rangement des objets de même propriétés en familles pour, par la suite, ne traiter qu'un seul représentant par famille.

Sommaire de cette page

>>> Approche

>>> Notion d'ensemble quotient

>>> Ensemble quotient – Définition et exemples

>>> Ensemble quotient – Formalisme mathématique

>>> Deux chemins

Débutants

Ensemble

Glossaire

Ensemble

Anglais: Quotient set, équivalence class

Jargon mathématique

Au cours de la scolarité, il est des mots qui n'évoquent pas grand-chose ou même qui induisent des idées fausses:

Primaire: fraction

Secondaire: vecteur

Économie: débit et crédit; passif et actif …

Supérieur: ensemble quotient, entropie …

Voir Jargon

Approche

haut

Division par 3

Sur ce tableau, on présente la division de N par 3 avec son quotient Q et son reste R (division euclidienne).

On observe que le reste boucle sur {0, 1 et 2}.
Et on note: N₃ = {0, 1 , 2}

On peut donc écrire un nombre sous la forme:
N = 3Q + {0, 1 ou 2}.

Ils sont donc de trois types, on dit de trois classes.

L'idée est de considérer un nombre N uniquement par son reste en oubliant le quotient. On note, par exemple: 10 ≡ 1 mod 3 (10 donne 1 lorsque divisé par 10; on lit: 10 est égal à 1 modulo 3; ou encore, 10 est congru à 1 mod 3)

Division par 2

Les nombres sont alors partagés en deux classes selon que le reste de la division par 2 est 0 ou 1.

Ce sont les nombres pairs et les nombres impairs.

Binaire

Division par 12

Oui ! Tout le monde compte les heures dans l'ensemble quotient de la division par 12.

Par exemple: 14 heures devient 2 heures, parce que 14 divisé par 12, reste 2.

Heures sur l'horloge

Notion d'ensemble quotient		haut
Si on prend l'ensemble N des nombres entiers, la relation R = "divisible par 2" séparent les nombres pairs des nombres impairs. L'ensemble des nombres est partitionné en deux classes d'équivalence: l'ensemble des nombres pairs et l'ensemble des nombres impairs. L'ensemble, ainsi partitionné (partagé, divisé) par R, est l'ensemble quotient de N par R. Avec les nombres entiers N (ou les nombres relatifs Z), chaque classe porte le nom du reste auquel elle appartient. 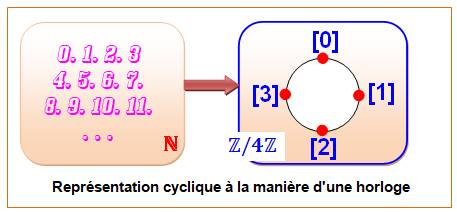Avec la division par 4, il y a quatre classes (boites) dans l'ensemble quotient par 4. On note: Pour encore mieux comprendre, il est possible de représenter l'ensemble quotient en tant qu'horloge. Représentation cyclique où les nombres se trouvent enroulés autour du cadran et les grands nombres se retrouvent automatiquement sur leurs représentants.
Dans l'ensemble infini des nombres entiers relatifs, on ne s'intéresse qu'aux restes possibles de leur division par n, on obtient l'ensemble quotient noté: qui comprend n éléments. Chaque nombre a une image (un correspondant) dans ce nouvel ensemble. Intérêt: les restes sont conservés suite à une addition ou une multiplication.	L'ensemble muni des deux opérations est un anneau commutatif. Anglais: Ring of integer modulo n denoted: .

Voir Brève 884

Ensemble quotient – Définition et exemples			haut
Une relation d'équivalence permet de regrouper des éléments similaires car partageant les mêmes propriétés. Comme les nombres divisibles par 2 ou par 3. L'ensemble source est alors partagé en plusieurs sous-ensembles. Chaque portion est une classe d'équivalence. Avec cette partition, l'ensemble de départ qui contient les classes devient l'ensemble quotient. L'ensemble de départ énumérant tous ses éléments et celui faisant état d'une partition (l'ensemble quotient) sont les mêmes. Sauf à composer des ensembles entre eux.		Les enfants en rangs par deux sont sur deux files: ceux à numéros pairs et ceux à numéros impairs. L'assemblée des enfants est répartie en deux classes, les pairs et les impairs. L'assemblée devient l'ensemble quotient pair/impair.
Le quotient E/𝓡 d’un ensemble E par une relation d’équivalence 𝓡 est par définition l’ensemble des classes d’équivalence modulo 𝓡.
L'ensemble quotient de E par est le sous-ensemble dont les éléments partagent les mêmes propriétés . On appelle ensemble quotient de E par la relation d'équivalence , l'ensemble des classes d'équivalence de E modulo
Exemple De la même couleur sur l'ensemble des feutres de ma trousse.	Il y a quatre (par exemple) classes d'équivalence pour cette relation : les rouges, les bleus, les jaunes et les noirs On forme ainsi l'ensemble quotient (quatre couleurs) .
Exemple Divisible par 2 sur l'ensemble des entiers.	Il y a deux classes d'équivalence pour cette relation : l'ensemble des entiers pairs, et l'ensemble des entiers impairs. On forme ainsi l'ensemble quotient (pair/impair) .
Exemple Parallélisme sur l'ensemble des droites.	Relation d'équivalence dont les classes sont les directions. Les classes sont alors en quantité infinie.
Exemple Construction de l'ensemble Q (les fractions) à partir de Z (les relatifs): *Prendre l'ensemble des couples de Z×N, La relation d'équivalence (a, b) R (c, d) lorsque ad – bc = 0 , Du fait de cette égalité pour les fractions, les classes qui en résultent sont celles des fractions semblables dont la fraction simplifiée et la représentative (la forme canonique). Ensemble quotient qui en résulte: l'ensemble quotient de Z en classes de fractions équivalentes. Son cardinal (quantité d'éléments) est bien entendu infini.**

Voir Congruences / Modulo

Ensemble quotient – Formalisme mathématique				haut
Décortiquons la définition mathématique de l'ensemble quotient.
La relation d'équivalence sur l'ensemble E est notée: Autrement-dit: la règle qui définit le partage de l'ensemble. En détail: l'ensemble (E) partagé ou partitionné (/) par la relation (~).
La classe d'équivalence est notée: La classe d'équivalence [x] d'un élément x de E est l'ensemble des y de E tels que x ~ y. Autrement-dit: [x] est le nom de la famille (de la classe) de tous les nombres partageant la même propriété. Formellement:
La classe [x] est un élément qui appartient à l'ensemble E partitionné par la relation (~).
Il est tel (barre verticale) que x appartient à l'ensemble E de départ. Sachant que x a pour correspondant (image ou représentant) [x]. Autrement-dit: x, transformé par la relation (~), atterrit dans la famille (la classe) [x].
Un ensemble où tous les représentants sont présents est appelé système de représentants des classes.
La transformation (l'application) de x en [x] s'appelle la projection canonique.

Propriété

On note que tout élément de E à un représentant: transformation surjective.

En revanche chaque élément [x] du système possède généralement de multiples antécédents dans E: transformation non-injective.

Rappel: tout sur cette page n'est valable que si la relation d'équivalence est binaire, réflexive, symétrique et transitive.

Deux chemins		haut
Reprenons la représentation classique d'une application f qui envoie un élément d'un ensemble de départ dans un ensemble d'arrivée. La flèche rouge montre comment, par exemple, le nombre 9 est associé au nombre 1 (même reste dans la division par 4). La mise en place de l'ensemble quotient qui partage l'ensemble des nombres en quatre montre un autre itinéraire (vert). Le nombre 9 fait partie de la classe [1] qui pointe vers le représentant de la classe le nombre 1 dans l'ensemble d'arrivée.
Vous trouverez ce schéma dans votre cours de maths. Il représente ni plus ni moins que celui du dessus. Les trois applications sont nommées f, [f] et π.

Bilan

Avec ces indications, vous avez le vocabulaire et les notions essentielles pour aborder des cours formels. Voir liens en fin de page.

Haut de page

Retour	Classes de congruence
Suite	Bon ordre Congruence Groupe cyclique Modulo Relation d'équivalence Table de Cayley
Voir	Numération binaire Dualité
Livre	Mathématiques L1 – Pearson Education – 2007
Sites	Ensemble quotient – Wikipédia Relation d'équivalence – ChronoMath Ensembles quotients – Gaétan Chenevier – Cours 11 pages Quotient set - Delta Function Equivalence Classes – Ted Sundstrom
Vidéo	Ensembles quotients – Maths adultes
Cette page	http://villemin.gerard.free.fr/Referenc/Outils/Outils/Structur/Quotient.htm