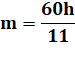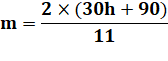|
||||||||||||||||||||||||||||
![]()
Précision
|
En
1721, George Graham construit une pendule dont
la précision atteignait une seconde par
jour. |
|
EN
utilisant des lasers très stables, on sait désormais comparer deux horloges
optiques via une liaison par fibre optique de 1 500 kilomètres (de Paris à
Brunswick, en Allemagne). Grâce à un aller-retour de la lumière, les
perturbations sont mesurées et compensées. Il
y a une vingtaine d'horloges optiques dans le monde, dernière générations des
horloges atomiques. Elles prennent moins d'une seconde de retard en 13
milliards d'années, l'âge de l'Univers. Janvier 2017 |
|
Question Pouvez-vous dire dans
quel contexte cette
égalité est réalisable: 9 + 6 = 3 Réponse En fait, il s'agit des
heures: 9 h + 6 h = 15 h ou 3 h En langage
mathématique, on écrit plutôt:
|
Question Pouvez-vous dire dans
quel contexte cette égalité est
réalisable: 8 + 6 = 8 – 6 Réponse Il s'agit également de
calculs sur les heures. Dans les deux cas, il est 2 heures.
|
Voir Calcul de l'horloge ou calcul modulo
/ Égalités
affolantes
Humour
|
Le juge au présumé voleur: – Ne niez pas, on vous a surpris dans l'escalier.
Vous descendiez une pendule. – Mais, monsieur de juge, je voulais la remonter
! |
|
Voir Pensées et Humour
Choix du sens de rotation des aiguilles
|
Horloge Les premières horloges furent inventées dans
l'hémisphère nord. Le soleil s'y déplace
d'est en ouest. Sur un cadran solaire, l'ombre du style se
déplace dans le même sens que le Soleil. Le sens des aiguilles de l'horloge a donc été
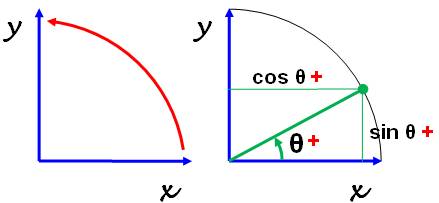
choisi par mimétisme avec celui du trajet du soleil. Maths Les mathématiciens disent que le sens horaire
est le sens négatif de rotation. Le sens positif étant le sens antihoraire. La raison: la rotation simple qui fait
passer des abscisses (axe des x) aux ordonnées (axe des y) est la rotation
antihoraire. De plus, un angle
orienté, compté à partir de l'axe x, produit un sinus et un cosinus
positif si l'angle est orienté en antihoraire. |
|
Voir Brève 61-1204
![]()
|
HORLOGE Deux sources d'émerveillement:
HORLOGE à folio Voici
un exemple qui me semble bien cl
|
Le balancier du haut lâche la roue dentée au
"goutte à goutte", cran par cran. |
Angl
Notez l
Horlogerie
se traduit par HOROLOGY
Pendules à l'heure
|
Remettre
les pendules à l'heure = remettre les
choses en place, dire les quatre
vérités, renvoyer dans ses vingt-deux. |
|
Une
pendule arrêtée est à l'heure deux fois par jour. Une
pendule qui retarde (ou avance) d'une minute par jour devra attendre 12 x 60 =
720 jours avant de se retrouver à la bonne heure. |
|
|
|
|
Pour les minutes
ce sera 59 qui donne14.
|
|
|
Deux
sabliers mesurant 4 et 7
minutes. Comment mesurer 9 minutes? |
|
|
||
|
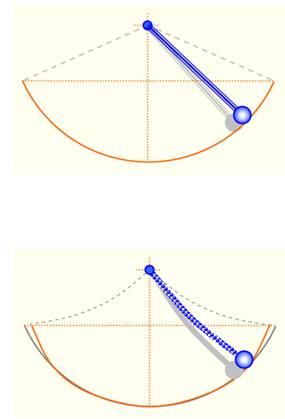
Cas du cercle
-
La période d'oscillation est dépendante de l'amplitude
du balancier. -
Les temps mis pour effectuer les oscillations ne sont
pas égaux, surtout si les amplitudes sont grandes. Cas de la cycloïde
-
Alors, la période des oscillations sera la même quelle
que soit l'amplitude. -
Propriété d'isochronisme de la cycloïde. |
|
|
|
L'abréviation
pendule a remplacé horloge à pendule il y a quatre siècles. On réserve le mot de pendules aux horloges
munies d'un balancier, par référence au pendule de la physique. |
|
Dans
la journée, combien de fois les aiguilles de l'horloge sont-elles à 90° l'une
de l'autre? |
|
|
||
|
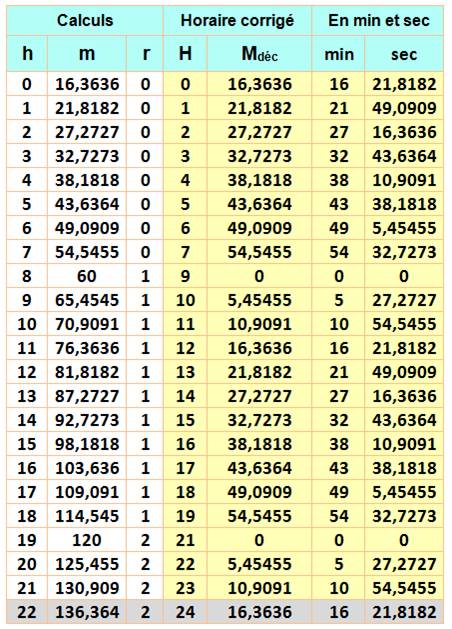
Recherche Quelle
sont les horaires pour lesquels les aiguilles sont
Combien
de fois dans la journée? La réponse n'est pas 24, mais 22 fois pour chacun de
ces cas. Pourquoi? Voyons cela. |
|
|
|
Mise en équation de la marche des
aiguilles La
référence pour compter les angles et la position des aiguilles à 0 h 00 min. La grande aiguille fait un tour toutes les 60 minutes.
Son angle (G) en degrés avec la référence est égal à: La petite aiguille avance plus lentement et elle
est positionnée au niveau de l'heure indiquée: |
60
minutes de marche pour la petite aiguille = 30°. Soit m/2 degrés pour m
minutes de marche. |
|
|
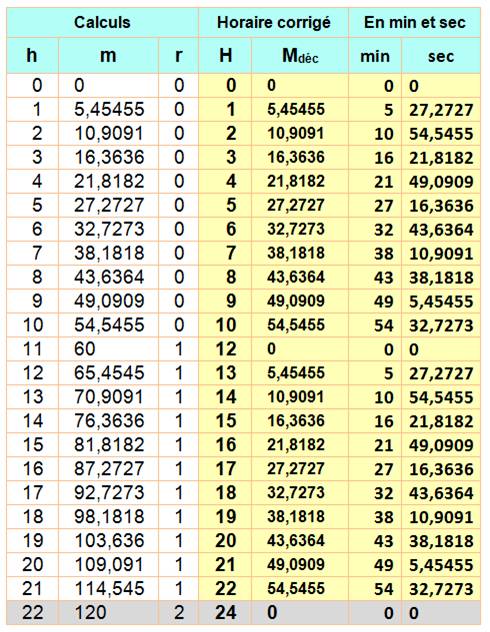
Aiguille superposées Nous
cherchons les valeurs telles que G = P Soit: 6m =
30h + m/2
Ex: h = 1 => m =
5,4545… Après 11
heures, les minutes dépassent 60; d'où une correction en retirant 60 minutes
et en ajoutant 1 aux heures. Remarquez
que les horaires de coïncidences l'après-midi sont ceux du matin. Au total
22 coïncidences. C'est le passage aux 11 heures 60 minutes qui occasionne un
saut éliminant une des occurrences. |
|
|
Aiguille à 90° Nous
cherchons les valeurs telles que G = P + 90 Soit: 6m
= 30h + m/2 + 90
Ex: h = 0 => m =
16,3636…
Le débordement des minutes intervient cette fois à 8h 60 min.
D'où 22 configurations seulement et non 24. Notez que cette fois
comme pour le cas précédent, on passe d'une configuration à la suivante en
progressant de: |
|
Allure
du graphe pour les aiguilles à 90°
|
Point noirs: les aiguilles sont à 90°. Points
rouges à 90° avec traversée de l'origine des angles en 0. Tracé vert: écart de 90° qui coupe la ligne 90° jusqu'à 8 heures. Tracé violet: écart 270° qui coupe la ligne 90° à partir de 9h C'est ce phénomène de retournement de la mesure
de l'angle qui explique les 11 points noirs au lieu de 12. |
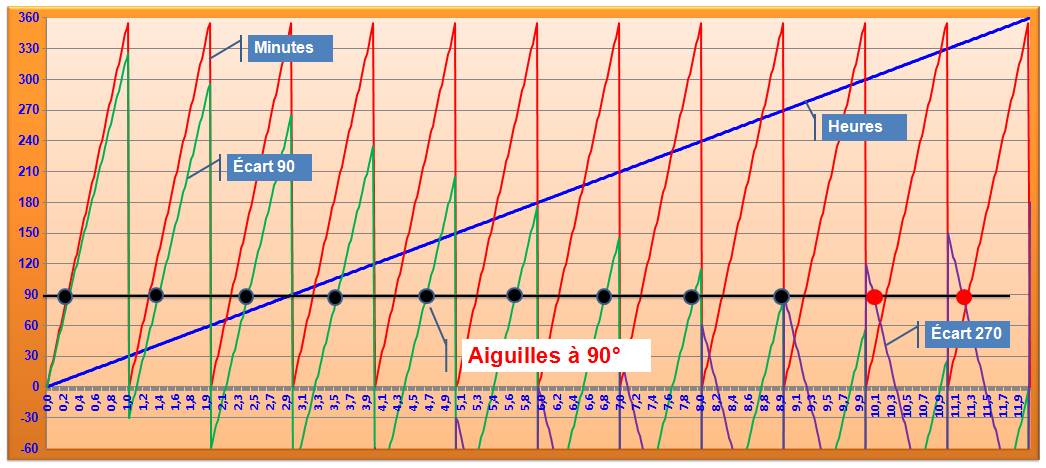
Le phénomène
de passage à travers l'origine des mesures des angles
qui explique le
fait qu'il n'y pas de configuration en 8 heures

|
Dans
la journée, combien de fois les aiguilles de l'horloge sont-elles à 90° l'une
de l'autre? À
raison de deux fois par heure, la réponse semblerait être 24. Un examen
attentif (ci-dessus)
montre que c'est 22. C'est 12h 45 qui crée le déraillement |
|
A stopped clock tells the correct
time twice a day. Une
horloge arrêtée donne l'heure deux fois
par jour. |
Voir Expressions avec deux / Pensées & humour
|
|
||
|
Analogie
avec le paradoxe du
nénuphar ou de l'escargot dans le puits Énigme L'horloge
a un gros problème de sensibilité à la température: le jour elle retarde de
1/2 minute le jour et elle avance de 1/3 de minute la nuit. Quand
l'horloge aura-t-elle atteint une minute de retard? |
Premier raisonnement En 24 heures, le bilan est: -1/2 + 1/3 = -1/6 Il faudra donc: 1 / (1/6) = 6 jours. Second raisonnement En y regardant de plus près, il y aura un jour où
le retard sera atteint du fait du retard pris le jour. En effet à la fin du jour 3, le retard est de 3 x 1/6 = 1/2 Or, durant le jour elle va retarder d'une
demi-minute: 1/2 + 1/2 = 1 minute de retard La bonne réponse est donc: Le retard de 1 minute est atteint à la fin du
jour du jour 4. |
|
|
Graphe Les flèches rouges montrent le passage à une
minute de retard soit en cumulé (raisonnement 1) ou en instantané
(raisonnement 2).
|
||
Historique – Origine de la division en 12
heures
|
Durant l'Antiquité,
les Égyptiens comptaient en douzaines. Les astronomes égyptiens avaient observé que la Lune avait 12 cycles
par an. Ils avaient aussi remarqué que douze étoiles se levaient à
intervalles réguliers pendant la nuit, à certaines époques de l'année, et ils
avaient divisé la nuit en douze parties. C'est naturellement que les premiers cadrans solaires, fabriqués en
Égypte il y a 3 500 ans, divisaient la journée en 12 parties. C'est ainsi que la journée comptait deux fois 12 heures. |
|
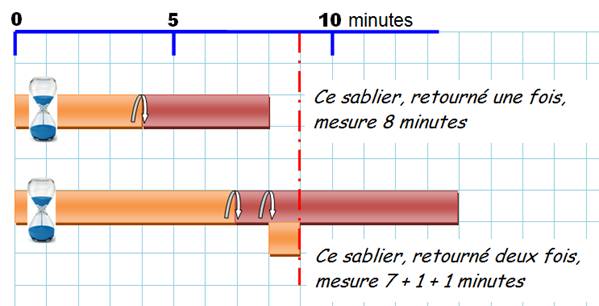
Deux sabliers mesurant 4 et 7 minutes. Comment
mesurer 9 minutes? Voici la solution en
image:
Au bout des 8 min
mesurées avec le premier sablier, l'astuce consiste à retourner à nouveau le
sablier de 7 min qui vient d'égrainer une seule minute. En le retournant, le
sable s'écoule à nouveau en une minute. |
Retour / Énigmes
de transvasement / Jeux et énigmes
![]()
|
Suite |
|
|
Amusements |
|
|
Voir |
|
|
DicoNombre |
|
|
Film |
|
|
Cette
page |
![]()