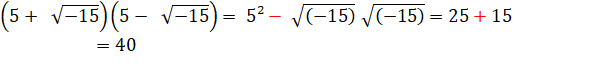|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Histoire des NOMBRES IMAGINAIRES D'abord révélés lors la
tentative de résolution des équations du troisième degré avec la nécessité de
traiter des racines de nombres négatifs. |
|
|
|
|
|
|
|
|
|
|
Il n'existe pas de nombre réel x dont le
carré soit –1. Les premiers mathématiciens prétendaient donc que cette
équation n'admettait pas de solution. Cardan (1501-1576) Cependant,
vers le milieu du XVIe siècle, Jérôme Cardan et ses
contemporains expérimentèrent des solutions d'équations faisant intervenir
des racines carrées de nombres négatifs. Pour résoudre l'équation: x (10 – x) = 40 Voir Variations sur cette équation Cardan suggéra d'exprimer le nombre réel 40 sous
la forme suivante:
Cardan
imagine que le produit des racines est négatif, d'où le signe + 15. Aujourd'hui (depuis Euler en 1777), on
pourrait écrire:
Bombelli (1526-1572) imagine une technique de calcul avec les
racines de nombres négatifs. Il se trouve confrontée à l'énigme suivante:
Leibniz, en 1702, fera
part de sa découverte à Christian Huygens
et à Pierre Varignon:
Jusqu'à cette époque, on cherchait à résoudre les
équations du troisième degré. Ce n'est que plus tard que cette technique de
calcul avec les racines négatives servira à résoudre les équations du second
degré dont le déterminant est négatif (à quelques exceptions près, comme
celle de Cardan indiquées ci-dessus). Euler, quant
à lui, introduisit en 1777, le symbole moderne i pour |
|
|
|
|||
|
William Rowan
HAMILTON
1805 Né à Dublin. 1835 Légitime l'emploi des nombres complexes en
mathématiques. 1843 Sa grande découverte:
les quaternions. 1865 Mort à Dunsink Voir Hamilton et ses contemporains
/ Nombres complexes En faisant des calculs avec les nombres complexes, il
s'intéresse à l'interprétation géométrique de l'addition et de la
multiplication dans le plan à 2 dimensions. Il
se demanda si avec des nombres hypercomplexes, on ne pourrait pas obtenir des
résultats analogues dans l'espace à 3 dimensions. Ses
recherches sont bien décrites par la célèbre anecdote avec son fils: Durant de
nombreuses années, HAMILTON avait espéré trouver une forme de multiplication
satisfaisante pour les triplets de nombres réels avec de bonnes propriétés.
En particulier: conservation de la multiplication des modules. Peu de temps
avant sa mort en 1865, il écrivit à son fils: "Tous les matins, alors
que descendais pour prendre le petit déjeuner, tu me demandais : 'Eh bien,
papa, est-ce que tu peux multiplier les triplets ?' J'étais toujours obligé
de répondre, avec un triste hochement de tête : 'Non, je peux seulement les
ajouter et les soustraire'." Finalement, HAMILTON a l'idée géniale de passer à un paramètre
de plus: "Ainsi naquit l'idée en moi d'admettre une quatrième dimension
pour calculer avec des triplets." (1843)
Il aboutit aux quaternions :
C'est Frobenius qui
démontrera en 1877, que les triplets ne peuvent pas exister! Euler, bien avant Hamilton, en 1748, il connaissait
la règle de multiplication des quaternions, sous la forme du théorème des
quatre carrés Gauss, lui aussi, connaissait la règle de calcul
des quaternions en 1819. |
|||
|
|
|
|
Gauss en 1831: il
n'existe pas d'autre système de nombres avec les mêmes lois fondamentales que
celles des nombres complexes. Hamilton octobre 1843:
découverte des quaternions par Hamilton. Encouragés par la
découverte des quaternions, de nombreux mathématiciens tentèrent de trouver
d'autres systèmes de nombres, d'autres algèbres hypercomplexes. Octonions ou
octavions décembre
1843, John Graves, puis indépendamment en 1845, Arthur Cayley construisent
les octonions ou octaves de Cayley, algèbre non associative. Bi quaternions: quaternions à
coefficients complexes introduits par Hamilton en 1853. Ils ne forment pas
une "vraie" algèbre (pas une algèbre à division). Clifford crée les algèbres associatives
qui portent son nom en 1878. Sur le plan théorique: Hamilton incapable de
prouver qu'il n'existe pas de système à triplets (algèbre à division
associative et commutative de dimension 3). Il reconnaît que
Gauss et Grassmann ont été les précurseurs de la découverte des quaternions. Frobenius en 1877: il
n'existe que 3 algèbres à division associative de dimension finie: Réels (R),
Complexes(C) et Quaternions (H). 1940: Cherche toutes les algèbres possibles Montre que, si on exige la commutativité, il n'existe
pas d'algèbre de dimension supérieure à 2 Il utilise la topologie
pour sa démonstration. Un début! Largement utilisée de nos jours Mazur et Gelfand 1938 et 1940: démontrent que R, C et H sont les seules
algèbres complètes (de Banach) |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()