|
Anglais: Casting out nines
![]()
|
Je me souviens que tous les nombres dont les chiffres donnent un total de neuf sont divisibles par neuf. Parfois
je passais des après-midi à le vérifier... Georges Perec |
|
Un chef-d'œuvre satisfait toutes les
Muses: c'est la preuve par neuf. Jean
Cocteau |
Voir Pensées
& humour
Magie!
|
Si
on soustrait ses chiffres à un nombre, le résultat est toujours divisible par
9.
Si
on soustrait un nombre et une de ses permutations de chiffres, la différence
est divisible par 9. Ex: 987 – 789 = 198 |
Voir Explications / Magie – Index
|
Définition |
PREUVE
|
|||||||||||||||||||||
|
Preuve p |
la plus connue, car la plus pratique.
Ce qui veut dire: Un nombre divisé par 9 donne le même reste
Un bon don des mathématiques!
Une addition, par exemple: Opération: 12 + 34 = 46 Images: 3
+ 7 = 10 |
|||||||||||||||||||||
|
Exemple pr |
Multiplication
Astuce! Pour vérifier l'égalité, souvenez vous que
les 9 disparaissent, mais vous pouvez en ajouter, notamment pour éviter les
nombres négatifs. Ex: 4045 – 2095 = 1950 En
ajoutant 9, l'égalité est bien là: –3 + 9 = 6. |
|||||||||||||||||||||
|
Attention
|
Avec
la multiplication ci- dessus, en inversant les chiffres: 42 x 12 = 288. Vous aurez un test positif (6 x 3
= 18 Une inversion (ou des inversions) de chiffres conduisent à un test
positif de la preuve par neuf. |
![]()
|
Angl |
Casting out nines.
|
|
Suite sur la preuve par 9 |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Vocabula/GlosP/Preuve.htm |
![]()
![]()
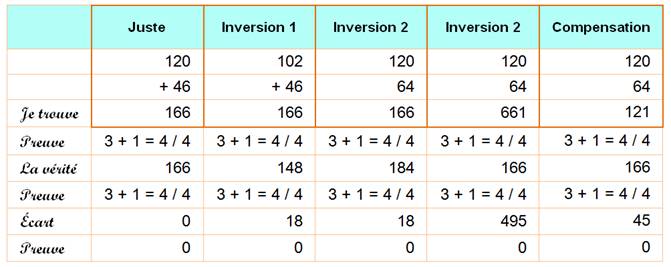
Cas de preuve par neuf vraie pour des opérations fausses
|
Énoncé |
|
|
Tableau d'exemples |
|
|
Conclusion |
Merci pour
cette contribution à Candice M. |
![]()
Rem
Vous
êtes très nombreux à m'écrire pour vous étonner de ces propriétés.
Tous les chiffres
|
Le nombre pannumérique
123456789 et toutes ses permutations
sont divisibles par 9. En effet la somme de leurs chiffres est multiple de 9. Il en va de même pour toute opération (addition,
soustraction et multiplication) comportant tous ces chiffres une fois ou k
fois chacun. Comme 12 + 34 + 5 + 6 + 7 + 8 + 9 = 81 >>> (Prudence avec la division !) |
|
Propriétés |
Exemple |
Preuve p |
Formul |
|
La somme des chiffres est un
multiple de 9 soit
9 ou 0 en preuve par neuf |
123 x 9 =
1107 1234 x 9 =
11106 4321 x 9 =
38889 |
=> 1 +1
+0 + 7 = 9 => 1 + 1
+ 1 + 0 + 6 = 9 => 3 + 8
= 11 => 2; |
P9 ( |
|
Ce nouveau nombre est divisible par 9 |
456 x 9
=4104 4104 + 4 +
1 + 0 + 4 = 4113 |
=> 4 + 1
+ 1+ 3 = 9 |
P9 (9N + |
|
Ce nouveau nombre est divisible par 9 |
789 – (7 +
8 + 9) = 765 |
=> 7 + 6
= 13 => 4 ; 4 + 5 = 9 |
P9 (N - |
|
Ce nouveau nombre est divisible par 9 |
987 – 789 =
198 |
=> 1 + 8
= 9 |
P9 (N - R) = 0 |
Voir Somme des chiffres des
puissances
|
Le tour |
|
-
Multiplier par 9. -
Retirer 5. -
Ajouter les chiffres. -
Recommencer pour obtenir un seul chiffre.
-
Trouvez un pays d'Europe commençant par cette lettre.
|
Voir
Solution
Voir
Autres magie avec 9: multiplication
pyramide / Tour simple /
Je devine
le chiffre / Transmission de
pensée
Nombres croissants et racine numérique
|
La racine numérique d'un nombre croissant multiplié par 9 est égale
précisément à 9. Explication 9 x abcde avec a < b < c < d < e Cela revient à multiplier par 10 – 1:
Qui s'écrit du fait que les nombres sont croissants: Cette simplification des termes deux à deux se nomment simplification par télescopage. |
12 x 9 = 108
=> RN = 9 123 x 9 = 1 107
=> RN = 9 1 234 x 9 = 11
103 => RN = 9 12 345 x 9 = 111
105 => RN = 9 45 x 9 = 405
=> RN = 9 456 x 9 = 4 104
=> RN = 9 4 567 x 9 = 41
103 => RN = 9 13 579 x 9 = 122
211 => RN = 9 2 468 x 9 = 22
212 => RN = 9 1 234 56 789 x 9 = 1 111 111 101
=> RN = 9 |
Voir Brève
602
![]()
![]()
|
Le
tour |
Exemple |
Explications |
|
|
123 456 1 111 104 1 111 099 1+1+1+1+9+9 = 22 2 + 2 + 4 |
Preuve par neuf donne 9 |
|
|
4 => D Danemark K = kiwi |
Seul pays avec D Seul fruit avec K |
|
Tour faisable
qu'une seule fois ! |
9 5 4 |
|
Donné
par Bernard Werber -
Nous les Dieux – 2004
Voir
Autres tours de magie
– Index
![]()