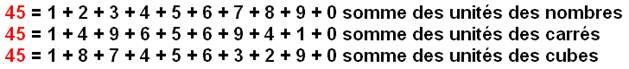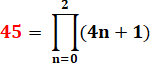Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 23/02/2025 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	40	41		42	43		44	45	46	47	48	49

Nombre 45	Maths 45	Culture 45	Curiosités 45
	Divisibilité par 45

Quarante-cinq

Fourty-five

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	10 1101
Bases	2314 558 3314
Romain	XL V

Suite

Somme des dix chiffres

45² = 2025, un nombre exceptionnel

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Caractérisation du nombre

Composé

Congruent

Coster

Déficient

Docile (amenable)

Harshad (45 / (4+5) = 5)

Idonéal

Impair

Interpremier (43, 45, 47)

Kaprekar

Narcissique de Keith

Mian-Chowla

Nombre 5-poli

Stirling 1

16-gonal (hexadécagonal)

Hexagonal (5^e)

Pascal C₁₀²

Triangulaire (6^e)

Nombre qui, en lettres, se contient lui-même:

QU4R4NTE + C1NQ

44 + 1 = 45

Une femme met quarante-cinq ans pour arriver à la trentaine.

Oscar Wilde

Voir Chiffres pour lettres / Nombres autocodes / Nombres alphabétiques /

Expressions avec 45 / Pensées & humour

CARTE D'IDENTITÉ
Nombre	Composé	Département	Loiret
Facteurs	45 = 3² x 5	Élément	Rhodium Rh
Pté Typique	45 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9	Mnémo	RÂLE
	Suite Maths		Suite Culture

Propriétés CULTURELLES
Anglais Allemand Espagnol Italien Romain Latin Grec	Forty-five Forty-fifth Fünfundvierzig Cuarenta y cinco Quarantacinque XLV Quadraginta quinque Pentatetraconta Voir Nombres et langues	Quarante-cinq Quarante-cinquième Quarante-cinquièmement Voir Orthographe des nombres

Géométrie	45° = 1 octant Angle de 45°. Part d'un cercle partagé en huit (quart divisé en deux). Le triangle rectangle isocèle possède deux angles à 45%
Balistique	45° Angle de jet pour une portée maximum du javelot.
Navigation	L'octant a un limbe de quarante-cinq degrés au lieu de soixante pour le sextant.
Sport	45 minutes = ¾ d'heure Une partie de football comprend deux mi-temps de 45 minutes.
	45 ans Limite d'âge moyen entre senior et vétéran. Quoique très variable selon les sports: entre 35 et 50 ans. Tableau pour la course à pied (trail) – Un exemple => Le changement de catégorie d’âge intervient au 1^er novembre de chaque année. Voir Catégorie (sports) - Wikipédia
	Une partie de pelote se joue en 45 points.
Jeux	45 s'affiche sur les calculettes avec autant de barrettes que l'indique la somme de ses chiffres.
	Carré latin  pannumérique Croix pannumérique
Littérature	Les Quarante-Cinq – Roman d'Alexandre Dumas – 1848.
Langue	Mittvierziger: Personne d'environ 45 ans chez les Allemands.
Musique	Disques 45 tours (correspond à 45 rotations par minute) Dans les années 70, les mange-disques étaient des électrophones à fente recevant les disques 45 tours Anglais: Single, car il y avait qu'une seule chanson par face. Voir 33 tours
Histoire	Guerre de 39-45: deuxième guerre mondiale (1939-1945). Voir Nombre 39
Social	45 ans de mariages: noces de Vermeil en France. Sapphire wedding anniversary in USA
Histoire	45 ans : les personnes nées en 1980 auront 45 ans en 2025 = 45². Le carré de leur âge. Événement rare.
Biologie	45 possibilités de descendances selon les groupes sanguins des parents.
	45 (de 40 à 50) grains de blé dans un épi. 300 à 1000 grains dans un épi de maïs
Consommation	Pernod 45: marque d'une boisson anisée dont le degré d'alcool est de 45 volumes.

Sport

45 jours 13 heures et 42 minutes Record du tour du monde à la voile en janvier 2012.

Propriétés MATHÉMATIQUES

Chiffres et numération

4, 5, 45, 54	Le nombre 45 est formé à partir de deux chiffres consécutifs. Quatre nombres formés avec les chiffres de 45.
45 => 4+5 = 2+0+2+5 = 9 45^2 = 2 025	La somme de ses chiffres est égale à la somme des chiffres du carré.
45 = 2+0+2+5 + 9+1+1+2+5 + 4+1+0+0+6+2+5 45^2 = 2 025 45^3 = 91 125 45^4 = 4 100 625		Narcissique de Keith Somme de ses chiffres à la puissance 2, 3 et 4 ou 1, 3 et 4. Voir Table des nombres de Keith
4510 = 1011012	Palindrome en binaire.
45 + 4 + 5 = 54	Mêmes chiffres lorsqu'augmenté de ses chiffres. Le plus petit tel motif
45 + 54 = 99 45 – (5 × 4) = 25 = 5² 45 × (5 × 4) = 900 = 30²	Devient repdigit lorsqu'ajouté à son retourné. et carré avec le produit de ses chiffres.
45 = 5 x (4 + 5) 54 = 6 x (5 + 4)	Seul nombre cinq fois somme de ses chiffres. Le suivant avec 6 est 54, son retourné.
4 + 5 = 5² – 4² = 9 = 3²	Propriété générale des nombres impairs.
45 = (4 + 4) 5 + 5 4545 4545 …45	Nombre de Coster (opérations utilisant deux fois ses chiffres). Motif valable pour tous les nombres à deux chiffres terminés par 5. Générateur d'une séquence de nombres de Coster se poursuivant sans cesse.

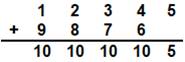
Addition et soustraction

45 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9	Partition unique avec les neuf chiffres. Somme maximum avec des chiffres différents. Constante du carré alphamagique. Progression arithmétique de raison 1. Plus petite somme des chiffres concaténés. Voir calcul simple de ce genre de sommes. Une des cinq sommes de nombres consécutifs >>>
		La somme des chiffres de tout nombre pannumérique est égale à 45. Les trois nombres de cette soustraction sont tous pannumériques et la somme de leurs chiffres est égale à 45. De là, Internet franchit le pas pour affirmer illicitement que 45 – 45 = 45 ! Voir Énigmes virales sur le Net

45 = 5 x 9	Nombre égal à neuf fois ses unités.
45 = 5 (4 + 5)	Seul nombre cinq fois la somme de ses chiffres.
45 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 9 x 10 / 2 = 1 + 5 + 9 + 13 + 17 = 1 + 15 + 29	Somme de tous les chiffres de 1 à 9. 9^e Nombre Triangulaire. 5^e Nombre hexagonal. 3^e Nombre figuré d'ordre 16 (hexadécagone).
45 = 1 + 2 + … + 9 = 5 + 6 + … + 10 = 7 + 8 + … + 11 = 14 + 1 5 + 16 = 22 + 23	Le plus petit nombre cinq fois somme d'entiers consécutifs. >>> Nombre 5-poli.
45 = 2 + 2 + 41 = 3 + 5 + 37 = 3 + 11 + 31 = 3 + 13 + 29 = …			Plus petit nombre douze fois somme de trois nombres premiers.
45 = 14 + 15 + 16		Nombre impair somme de trois impairs consécutifs. Tous les nombres impairs divisibles par k sont sommes de k nombres impairs. Voir Tableau

Le nombre 45 comme somme de k impairs consécutifs

Voir Unités des puissances
45 = (10+2) + (10-2) + (10x2) + (10/2)	Somme des quatre opérations.
45 = 4 + 20 + 21 = 5 + 12 + 28 = 7 + 8 + 30 & 4 x 20 x 21 = 5 x 12 x 28 = 7 x 8 x 30 = 1 680			Trois tripartitions dont les produits des termes sont identiques.
		Le nombre 45 auquel on ajoute son cinquième se retourne (54). Le seul à deux chiffres. Ce motif se répète sans fin avec 4545, puis 450045, puis deux zéros en plus pour la suite. Même opération pour 495, puis 4995, puis un 9 intercalé à chaque fois. Même type de motif sans fin avec 4356 + 4356 / 2 = 6534

Multiplication

	Factorielle quadruple de 2 = (4x0+1) (4x1+1) (4x2+1) = 1 x 5 x 9
45 x 987679 = 44445555 45 x 2222000 = 99990000	Deux seuls nombres en aaaabbbb divisibles par 45. Objet d'une énigme.

Division, diviseurs

	Les 20 nombres de 100 à 999 divisibles par 45 (par 5 et par 9). Il y en a 200 pour les nombres de 1 000 à 9 999 et, plus généralement: il y en a 2x10^k–1 pour les nombres en 10^k.
Facteurs de 45 = {3, 5} + 3 => {6, 8} qui divisent 45 + 3 = 48	Nombre facteur-3-diviseur.
	Plus petite paire de nombres successifs avec six diviseurs avec le nombre 44.
PGCD(45, 2k+1 < 45) = 1	Les 11 nombres impairs premiers avec 45 sont effectivement premiers.
45 – 2^k avec k de 1 à 5 => 43, 41, 37, 29, 13	Sont tous premiers.

Nombre 45 et puissances

45 = 3² + 6² = 2² + 4² + 5²	Nombre binomial. Somme de carrés de nombres distincts. Deux seules en deux ou trois termes.
45 = 1^3 + 1^3 + 2^3 + 2^3 + 3^3	Somme de cubes.
45 = 23² – 22² 9² – 6² 7² – 2²	Motif général pour tout nombre impair. Différence de deux carrés sous trois formes. 45 est le plus petit; le suivant est 48.
45 = 4^3 – 3^3 + 2^3	Somme de trois cubes. Notez la progression des trois nombres au cube.
45 = 6! / 4² = 720 / 16 = 6! / 2^4	Factorielle divisée.

Puissances de 45

45² = 2025		Un nombre exceptionnel
45² = 20 25 et 20 + 25 = 45 45^3 = 91 125 et 9 + 11 + 25 = 45 45^4 = 4 100 625 et 4 + 10 + 06 + 25 = 45		Nombre de Kaprekar d'ordre 2, 3 et 4. Rare, sinon le seul. Suite en 5 et 6 avec nombres négatifs et nombre 2025 = 45²
45² = 27^2 + 36^2 = 36^2 + 9^3 = 27^2 + 6^4 = 36^2 + 3^6	Sommes: carré plus puissance, dont une puissance 6.
45^3 = 135² + 270² = 54² + 297²	Cube somme de deux carrés.
	Bicarré concaténation de trois carrés.
45^4 = 1^4 + 2^4 + 12^4 + 24 + 44^4 = 1^4 + 8^4 + 24^4 + 36^4 + 38^4 = 4^4 + 4^4 + 26^4 + 27^4 + 42^4= 6^4 + 6^4 + 18^4 + 36^4 + 39^4 = 12^4 + 18^4 + 24^4 + 27^4 + 42^4= 18^4 + 18^4 + 27^4 + 36^4 + 26^4	Bicarré sommes de cinq bicarrés. dont les trois dernières sont des multiples de 5 et de 15. Seule les deux premières comportent des termes distincts.
45^6 = 8 303 765 625 & 8+3+0+…+2+5 = 45	Nombre NESCHIP.
2^45 = 35 184 372 088 832	Plus petite puissance de 2 avec une suite de trois 8 de suite.

Curiosités

		Plus petit nombre dont la période du développement de la fraction est 2.
		Une partition singulière du nombre 45 et relation de chaque terme avec les quatre opérations et le nombre 2.
45 = 9 + 9 + 9 + 9 + 9		Le record de la somme des chiffres des nombres jusqu'à 100 000. Suivant: 199 999 avec la somme 46.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 123456789 x 5 = 246913578 123456789 / 2 = 61728394,5		La somme pannumérique vaut 45. Deux opérations avec des nombres pannumériques (somme 45) de chaque coté de l'égalité.
e^45 – Entier = 0,03479… Entier = 34934271057485095348 = 3,49… 10^19			Exponentielle proche d'un entier.
6² – 5² = 11 56² – 45² = 1 111 556² – 445² = 111 111 5556² – 4445² = 11 111 111	Différences de carrés. Calcul: a² – b² = (a + b) (a – b) 56² – 45² = (56 + 45) (56 – 45) = 101 x 11= 1 111 Voir Somme de carrés / Différence de carrés

Équation

x	2x	x / 2	Différence
2	4	1	3
4	8	2	6
6	12	3	9
30	60	15	45

Trouver un nombre dont la différence entre le double et la moitié est 45.

Mise en équation

2x - x/2 = 45

4x - x = 90

x = 30

On aurait pu choisir n'importe quel nombre plutôt que 45 à condition qu'il soit divisible par 3.

Dénombrement, jeux et curiosités

45 pour {10, 20, 21, 30, 31, 32, 33, 40 …}		Quantité de nombres dominants à gauche à deux chiffres.
		Jeu du quatre 4.
		Coefficient du binôme ou nombre de Pascal. Quantité de combinaisons de 2 ou 8 parmi 10. Exemple: 10 candidats aux élections. Il faut 45 débats pour les avoir tous deux à deux.
45	Il y a 45 nombres dont l'unité est strictement plus grande que tous les autres chiffres pour les nombres de 1 à 99. Liste: 1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 13, 14, 15, 16, 17, 18, 19, 23, 24, 25, 26, 27, 28, 29, 34, 35, 36, 37, 38, 39, 45, 46, 47, 48, 49, 56, 57, 58, 59, 67, 68, 69, 78, 79, 89. Voir Nombre 285

Décimales

Curiosité en pi et exponentielle. Le plancher de ce nombre vaut 45.

Autour du nombre

45°	Demi-angle droit. Pente de la droite: y = x
45°	Angle de vision d'un côté d'un octogone depuis son centre.
45°23'	Angle particulier dans les cristaux de calcite

Équation de degré 45 résolue par François Viète (1593)

En 1593, Adrianus Romanus (Adrien Romain, mathématicien flamand) propose cette équation à ces contemporains.

45x – 3795x³ + 95634x⁵ – 1138500x⁷ + 7811375x⁹ – 34512075x¹¹ + 105306075x¹³ – 232676280x¹⁵ + 384942375x¹⁷ – 488494125x¹⁹ + 483841800x²¹ – 378658800x²³ + 236030652x²⁵ – 117679100x²⁷ + 46955700x²⁹ – 14945040x³¹ + 3764565x³³ – 740259x³⁵ + 111150x³⁷ – 12300x³⁹ + 945x⁴¹ – 45x⁴³ + x⁴⁵ = N

François Viète (1540-1603), mathématicien français, est le premier à la résoudre. Il a rapidement reconnu que l'équation était satisfaite par la corde d'un cercle de rayon 1, sous-tendant un arc de 8° (2Pi/45). C'est la solution dont disposait Romanus. En fait, Viète a trouvé les 22 autres solutions positives. Il en existe autant en négatifs, mais non reconnues en ce temps là. Une amitié entre les deux mathématiciens se noue. Les solutions de Viète sont publiées en 1595 sous le titre: Ad problema quod omnibus mathematicis totius orbis construendum proposuit Adrianus Romanus, responsum.

À la fin du texte, Viète propose de résoudre le dernier problème (le dixième) du traité perdu d'Apollonius: tracer un cercle tangent à trois cercles donnés.

La résolution de ces deux problèmes vaut à Viète une notoriété immédiate parmi les mathématiciens de l''époque et du futur. C'est lui qui donnera la valeur de Pi avec cette formule faite de racines imbriquées:

Voir Brève 666

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 0, 1, 1, 0, 1] 3, [1, 2, 0, 0] 4, [2, 3, 1] 5, [1, 4, 0] 6, [1, 1, 3] 7, [6, 3] 8, [5, 5] 9, [5, 0] 10, [4, 5] 11, [4, 1]	12, [3, 9] 13, [3, 6] 14, [3, 3] 15, [3, 0] 16, [2, 13] 17, [2, 11] 18, [2, 9] 19, [2, 7] 20, [2, 5] 21, [2, 3]	22, [2, 1] 23, [1, 22] 24, [1, 21] 25, [1, 20] 26, [1, 19] 27, [1, 18] 28, [1, 17] 29, [1, 16] 30, [1, 15]	8, [5, 5] 14, [3, 3] 44, [1, 1]

Voir Bases / Brésiliens

Suite	Voir le menu en haut de page Divisibilité des nombres par 45 Nombre 46
Orientation	DicoNombre
Voir	Billard Catalan Cristaux Cycle de vie Grille magique Palindrome retard Premier Primorielle Sous-factorielles
Site	François Viète – Wikipédia
Cette page	http://villemin.gerard.free.fr/NombDico/Nb30a50/Nb45-49.htm

Quelques liens dans ces pages

Arithmétique & Calcul >>> CARRÉ et PRODUIT >>> DIFFÉRENCES DE CARRÉS >>> DIVISEURS PROPRES >>> DOUBLE & MOITIÉ >>> DIVISIBILITÉ par 49 >>> NOMBRES 48 & 49 >>> PROGRESSION ARITHMÉTIQUE >>> NOMBRE 45 >>> NOMBRE 46 >>> NOMBRE 47 >>> NOMBRE 48 >>> NOMBRE 49 Jeux et puzzles >>> CARRÉ LATIN >>> CARRÉ pour MAGICIEN >>> FRACTIONS ILLICITES >>> JAVELOT >>> Les 9 ENFANTS

Humour Logique Géométrie >>> TRIANGLES dans le TRIANGLE Multimédia - Informatique Économie Physique - Chimie - Biologie >>> ARGENT >>> CHROMOSOMES >>> CRISTAL Cosmologie Philosophie - Religion - Littérature >>> SHAKESPEARE Linguistique Culture générale >>> ANNÉE la PLUS LONGUE >>> JEUNE PRÉSIDENT