|
||||||||||||||||||||||||||||||||||
![]()
|
SUITE DE FIBONACCI Formule de Binet Comment calculer
directement les nombres de Fibonacci sans avoir à calculer tous les
précédents. Généralisation des nombres de Fibonacci. En
1834, Jacques Binet (1786-1856)
publie une formule qui donne le énième nombre de la suite de Fibonacci. Elle
était connue d'Abraham de Moivre (1718), Daniel Bernoulli, et démontrée par
Leonhard Euler (1765). La
formule de Binet pour
calculer un nombre de Fibonacci de rang n >>>
En
pratique pour calculer un nombre de Fibonacci de
rang n élevé >>>
|
Voir Fibonacci, Binet et nombre d'or
|
|
||||
|
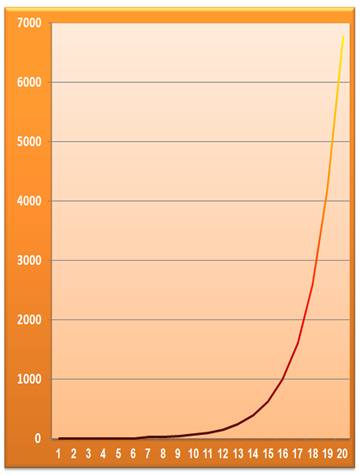
La suite
de Fibonacci a l'allure exponentielle d'une suite
géométrique. |
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …] |
|||
|
Forme
générique d'une suite
géométrique: |
|
|||
|
Selon la
relation de récurrence de la suite de Fibonacci. |
|
|||
|
En divisant
par a.rn-1 |
|
|||
|
Équation du second degré dont
les racines sont: |
|
|||
|
D'une
suite géométrique nous passons à deux possibles. |
|
|||
|
Si la
relation de récurrence est satisfaite, reste à vérifier que les conditions
initiales sont respectées. |
F0 =
0; Or, G0 = a; Ce qui veut dire que a = 0; ce qui est impossible; il n'y aurait
pas de suite géométrique. |
|||
|
Observation
conduisant à profiter des deux suites trouvées pour former une nouvelle suite
qui satisfait toujours la récurrence. |
Gn+1 = Gn + Gn-1 Hn+1 = Hn + Hn-1 Gn+1 – Hn+1 = Gn – Hn + Gn-1
– Hn-1 |
|||
|
Notre
formule prend forme: |
|
|||
|
F0 = G0 – H0 =
a(1 – 1) = 0 |
||||
|
Autre
condition initiale: F1 = 1 |
|
|||
|
Formule
finale: |
|
|||
|
|
||
|
Formules développées Note: ici, nous avons la différence entre les
deux termes en phi qui, divisée par racine de 5, donne un entier. La somme, sans cette division, donne
aussi un entier >>> |
|
|
|
Formules condensées Avec
le nombre d'or.
et
l'opposé de son inverse
|
Toutes
ces formules donnent bien ce résultat, avec F0
= 0: [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,
377, 610,…] En
remplaçant la puissance n par n + 1, vous trouverez: [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,
610, 987] avec
F0 = 1. |
|
Voir Table des nombres de Fibonacci
/ Généralisation de la suite de
Fibonacci
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
y = 0,4547 e0,4807
x
Exemple
|
|
|
Fibonacci
et exponentielles On
retrouve les plus petites valeurs de Fibonacci en utilisant la fonction
exponentielle des nombres successifs de la façon suivante:
Les
valeurs successives: 1, 2, 3, 5, 8,
13, 21, 34, 55 et 91, … Pour n =
9, la valeur est 91 au lieu de 89; et la formule
diverge ensuite. Grande
loi de Guy Coïncidence
parfois citée comme exemple de la loi de Guy
concernant les petits nombres. Elle dit que: Il n'y a pas
assez de petits nombres pour satisfaire toutes les exigences qui leur sont
demandées. "There
aren't enough small numbers to meet the many demands made of them". Petite
loi de Guy Lorsque
deux nombres paraissent semblables, ce n'est pas forcément le cas. When two
numbers look equal, it ain't necessarily so! |
Voir Mersenne en Puissance / Partition du cercle / Richard Guy
|
|
|
|
2, 22 , 23 , 24 , 25 ….
|
|
|
Arrondi
(Gn) = Fn En pratique, pour calculer un nombre de Fibonacci
avec la formule de Binet, seul le calcul du premier terme suffit. Exemple
de calcul de F10
avec la calculette:
=> 54,992… Arrondi à
55. |
|
|
|
|
|
Cette somme est un entier
qui est lié aux nombres de Fibonacci.
|
|
![]()
|
|
||
|
Le
coefficient en racine de 5 dans la formule de Binet est rendu quelconque. |
|
|
|
FIBONACCI La suite
de Fibonacci est obtenue avec la formule de Binet. |
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,
610,…] F1
= 1, F2 = 1 … |
|
|
Programme Maple Notes: on commence
bien la boucle avec n = 1. Le coefficient en racine de cinq (rc) est appliqué en plus sur le premier terme
et en moins sur le second Les nombre entiers de la suite sont obtenus en
arrondissant (round) les valeurs calculées |
|
|
|
LUCAS On
retrouve la suite
de Lucas avec les coefficients (1, 1) Note: deux versions au départ: F1 = F2
= 2 ou F1 = 1 et F2 = 3. |
[1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521,
843, 1364 …] F1
= 1, F2 = 3 … |
|
|
Programme Maple Note: Cette fois les coefficients sont : |
|
|
Voir Convergence
du rapport de ces suites (nombre d'or et ses cousins)
Merci à Jamila B. pour ses remarques
|
|
|||
|
Prenons
la suite construire à partir de a = 2 et b = 5. |
2, 5, 7, 12, 19 … |
||
|
Quelle
est la "formule de Binet" qui permet de construire cette suite ? La solution consiste à ajouter deux suites (Fibonacci
+ Lucas) chacune dans une certaine proportion. |
Cette formule résulte d'un calcul sur une suite récurrente à deux
termes. (Voir les sites en référence). |
||
|
Pour note
exemple |
|
||
|
En effet |
|
||
|
Calcul du
énième terme |
|
||
Merci à Jean-Pierre G pour ses remarques
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Sites |
|
|
Cette page |
![]()