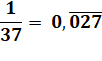|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES PÉRIODIQUES DICHOTOMIE Somme
des demi-périodes en 99…9 Nombres de Midy ou nombres
Dichotomiques |
|
|
Le développement décimal
de la fraction 1/7 est périodique. La somme de la première demi-période
(142) et de la seconde demi-période (857) est égale à 999. Nombreux sont les nombres
premiers comme 7 qui somment en un repdigit
en 9. Qui sont les nombres
dichotomiques? Notez qu'on a aussi: 14 + 28 + 57 = 99 avec les tiers de période. |
|
Voir Cartographie
des nombres périodiques / Nombres réels
|
|
||
|
Calculons
le développement décimal de la fraction 1/7. La période est 142857 avec une
longueur de période (LC) de six
chiffres. La longueur maximale pour la
période (p – 1 = 7 – 1 = 6). En
partageant cette période en deux moitiés égales (dichotomie) et en sommant les
deux nombres, on obtient 999. Dans tous les cas, la somme étant en 99…9, la période est divisible
par 9. Mieux, la somme est effectuée sans retenue: chaque chiffre de la
première partie trouve son complément
à 9 au même rang dans la seconde partie. Cette
opération se reproduit pour tous les nombres premiers de ce tableau avec une
somme comportant LC / 2 fois le chiffre
9. Avec les
premiers 7, 13 et 19, dont la période est divisible par 3, la propriété
s'étend au tiers de somme: 1/7 => 14 + 28 + 57 = 99 1/13 => 7 + 69 + 23 = 99 1/19 => 52631 + 578947 + 368421 = 999999 Cette fois les additions sont avec retenues. |
|
|
|
Pour le
nombre premier suivant, pas de chance, la longueur de la période n'est pas
paire; elle n'est pas partageable en deux moitiés égales. Par
contre, la somme est en 9 pour les tiers. |
3225 + 80645 + 16129 = 99999 |
|
|
Le
suivant a une période de 3 chiffres dont la somme (somme des tiers) est 9. |
0 + 2 + 7 = 9 |
|
|
Le
suivant a une période de cinq chiffres. Aucune propriété particulière, sinon
la somme des chiffres qui est divisible par 9. |
Somme des chiffres: 18 |
|
Bilan
|
On
s'intéresse au développement décimal de l'inverse d'un nombre premier:
|
|
|
||
|
|
Initialisation avec restart. Ouverture des logiciels de théorie des nombres. Le nombre premier au départ sera égal à 5 et nextprime
donne le suivant (7). On lance une boucle de cinq itérations. Calcul des chiffres de la période P. C'est le quatrième élément de
l'expansion de 1/p obtenu avec l'instruction dédiée: pdexpand. Calcul des deux demi-sommes avec l'instruction somme (sum). La première de 1 à L/2 et la seconde de L/2 +1 à L. On affiche successivement: le nombre premier p, la longueur L de la
période, les deux demi-sommes Si et S2, puis leur somme. |
|
Voir Programmation
– Index
|
|
||
|
Théorème de Midy
(1836) – 1/p Si le
développement décimal de 1/p a une période de longueur paire, alors les
motifs des deux demi-périodes ont pour somme un repdigit en 9. |
|
|
|
Théorème de Midy – n/p L'inverse
d'un nombre premier (1/p) ou ses
multiples (n/p). On se limite à n
de 1 à p – 1. Au-delà, on retrouve les mêmes propriétés mais la fraction
comporte une partie entière. Ce nombre
(n/p) a un développement décimal
périodique. |
Pour un nombre premier p différent de 2 et 5. Si la longueur de la période est paire L = 2k:
|
|
|
Théorème de Midy
(complet) Soit n et
p deux nombres entiers positifs, avec p > 1, PGCD(p,
10) = 1, PGCD(p, n) = 1 et 0 < n
< p. Si
le développement décimal de n/p a une
longueur de période paire, notée:
|
Alors, pour
Traduction: cette
somme exprime que chaque chiffre de la première partie trouve son complément à 9 dans la
seconde partie. |
|
|
Théorème de 0. Mathieu (2002) Avec p
> 7, la décimale (p + 1)/ 2 est 0
ou 9, valeur dépendante de p mod 40. |
|
|
Anglais: The nines property: when the period length is even
and the
period is broken into two halves of equal length
which
are then added, the result is a string of 9’s.
Étienne Midy (vers 1773-1846) et les autres …
|
Mathématicien français qui a été professeur à Cahors, Orléans
et Nantes. Auteurs d'une quinzaine de publications >>> Son article qui a donné le théorème de Midy comporte 21 pages. Les autres mathématiciens qui se sont intéressés à
cette question: H. Goodwyn (1802), Dikson (1952),
Leavitt (1967), Shrader-Frechette
(1978). C'est Ginsberg (2004) qui a étendu le théorème aux
périodes divisible par 3. |
Voir Contemporains
|
|
||
|
Observations On
pourrait être tenté d'explorer les fractions avec un dénominateur composé. Ça ne
marche pas toujours! |
Pour tous les cas où ça marche (jaune), on a PGCD(p,10k – 1)
= 1 Et une autre valeur dans les cas où ça ne marche pas. C'est le troisième cas du théorème de Midy. |
|
|
Nombres dichotomiques |
Un nombre
dichotomique est un nombre dont le développement décimal de son inverse
présente une période partagée en demis sommant en 99…9; la somme des deux
demi-périodes est égale à un repdigit en 9. Les
nombres premiers comme les nombres composés ne sont pas tous dichotomiques.
Parmi les nombres de 1 à 1000, seuls 390 sont dichotomiques. Par
contre, tous ceux caractérisés par le théorème de Midy
sont dichotomiques. Les
premiers nombres dichotomiques (dont premiers en rouge): 7, 11, 13, 14, 17, 19,
22, 23, 26, 28, 29,
34, 35, 38, 44, 46, 47, 49, 52 … Suite >>> |
|
|
|
||
|
|
Deux procédures (sorte de fonction) qui calculent les deux
demi-périodes S12 et S22. En n, on trouve une liste de chiffres dont la quantité est q (calcul
avec nops). L'instruction somme (sum) reconstitue le
nombre classique à partir des chiffres multipliés pat la puissance de dix
associée. La première demi-période prend les chiffres de 1 à q/2; et la seconde
de q/2+1 à q. La procédure Midy interroge les deux
procédures précédentes pour renvoyer le nombre n que s'il est dichotomique. En s on place les chiffres de la période de 1/n. C'est le quatrième
élément de l'expansion de 1/n, obtenue par l'instruction pdexpand
du logiciel numtheory. Le op
initial permet de se débarrasser du texte qui accompagne la réponse de pdexpand. Si la longueur de la période est paire (son modulo 2 = 0), alors Si la somme des demi-périodes est égale à 99…9 (= 10k – 1),
alors le nombre n est retourné comme validé dichotomique. Le programme principal balaye les nombres de 2 à 100 et forme la liste
S des nombres dichotomiques. On affiche L et sa quantité d'éléments. En bleu, résultat du traitement: 39 nombres dichotomiques de 2 à 100,
commençant par 7, 1, 13 … |
|
Voir Programmation
– Index
|
|
||
|
Un nombre
trichotomique est un nombre dont le développement
décimal de son inverse présente une période partagée entiers sommant en 99…9;
la somme des trois tiers de périodes est égale à un repdigit en 9. Contrairement
aux nombres dichotomiques, la somme comporte des retenues dans la majorité
des cas. |
Les premiers nombrs trichotomiques:
|
|
![]()
Analyse de quelques premiers
longs
|
1/17 |
= 0,0588235294117647… |
Somme |
16 |
|
|
0 + 5 + 8 + …+ 7 = |
=
9 x 8 |
1 |
|
|
05 + 88 + 23 + 52 + 94
+ 11 + 76 + 47 = |
=
99 x 4 |
2 |
|
|
0588 + 2352 + 9411 +
7647 |
=
9 999 x 2 |
4 |
|
|
05882352 + 94117647 |
=
99…98 x 1 |
8 |
|
1/19 |
= 0,052631578947368421… |
Somme |
18 |
|
|
0 + 5 + 2 + 6 + … + 1 |
=
9 x 9 |
1 |
|
|
05 + 26 + 31 + 57 + …
+ 36 + 84 + 21 |
=
99 x 4 |
2 |
|
|
052 + 631 + 578 + 947 +
368 + 421 |
=
999 x 3 |
3 |
|
|
052631 + 578947 + 368421 |
=
99…96 x 1 |
6 |
|
|
052631578 + 947368421 |
=
99…99 x 1 |
9 |
|
1/23 |
= 0,0434782608695652173913… |
Somme |
22 |
|
|
0 + 4 + 3 + 4 + … + 3 |
=
9 x 11 |
1 |
|
|
04 + 34 + 78 + … + 13 |
=
99 x 4 |
2 |
|
|
04347826086 + 95652173913 |
=
99…911 x 1 |
11 |
|
1/29 |
= 0,0434782608695652173913… |
Somme |
28 |
|
|
0 + 4 + + 3 + 4 + … +
3 |
=
9 x 14 |
1 |
|
|
04 + 34 + 47 + … 13 |
=
99 x 7 |
2 |
|
|
=
9999 x 4 |
4 |
|
|
|
=
99…97 x 2 |
7 |
|
|
|
=
99…914 x 1 |
14 |
|
1/47 |
= 0,0212765957 4468085106
3829787234 0425531914 893617… |
Somme |
46 |
|
|
0 + 2 + 1 + 2 + 7 + …
+ 7 |
=
9 x 23 |
1 |
|
|
02 + 12 + 76 + 000 +
17 |
=
99 x 9 |
2 |
|
|
=
99…923 x 1 |
23 |
|
1/97 |
= 0,0103092783 5051546391
7525773195 8762886597
9381443298 9690721649 4845360824 7422680412 3711340206 185567… |
Somme |
96 |
|
|
0 + 1 + 0 + 3 + 0 + 9
+ … + 7 |
9
x 48 |
1 |
|
|
01 + 03 + 09 + 27 + …
+ 67 |
99
x 24 |
2 |
|
|
010 + 309 + 278 + … +
567 |
999
x 16 |
3 |
|
|
0103 + 0927 + 8350 + …
+ 5567 |
9
999 x 12 |
4 |
|
|
010309 + 278350 + 515463
+ … + 185567 |
99…96
x 8 |
6 |
|
|
01030927 + 83505154 + …
+ 06185567 |
99…98
x 6 |
8 |
|
|
99…912
x 4 |
12 |
|
|
|
99…916
x 3 |
16 |
|
|
|
99…924
x 2 |
24 |
|
|
|
99…932
x 1 |
32 |
|
|
|
99…948
x 1 |
48 |
Bilan
|
En
prenant 1/97 comme exemple, la période 96 a pour diviseurs (1, 2, 3, 4, 6, 8,
12, 16, 24, 32, 48 et 96). En partageant la période par ces nombres, on
obtient des nombres dont la somme est toujours divisible par un repdigit en 9
ayant autant de chiffres que p divisé par le diviseur. Certains
cherchent la théorie de ces motifs. Notez que les chiffres portés en rouge
sont des anomalies. On ne retrouve pas les diviseurs de la colonne de droite
dans le produit de la colonne juste à gauche. Pourquoi? |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Nombre/aaaCycli/NbCycDic.htm
|
![]()