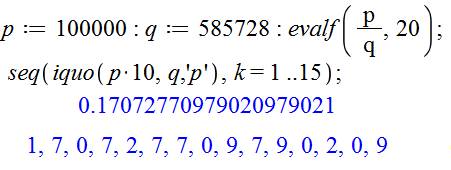|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES
PÉRIODIQUES Extraction des décimales
Comment
extraire les chiffres un à un. Comment
extraire la période par programmation. |
|
|
|
|
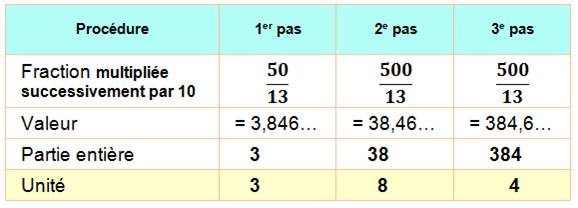
Procédure On
cherche un moyen d'isoler les chiffres du développement d'une fraction par
exemple au moyen d'un tableur. Pour
cela, la solution la plus simple consiste à:
Exemple: 5 / 13 = ….
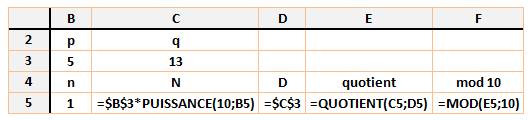
Formules utilisées
|
|
|
Recherche des chiffres d'un nombre décimal |
|
|
|
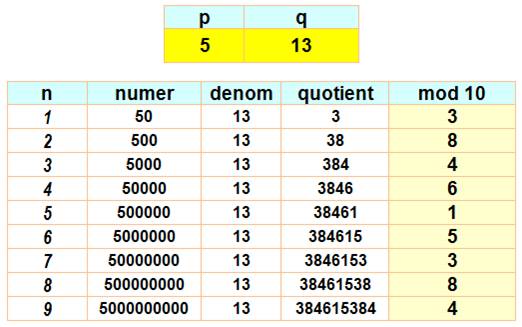
Programme selon la procédure vue ci-dessus
|
Programme qui calcule le nombre décimal à partir d'une fraction et en
isole les chiffres. |
|
|
Explications La
première ligne efface tout dans la mémoire (restart) et positionne p et q à 5
et 13, le numérateur et le dénominateur de la fraction étudiée. La
deuxième ligne traduit une des lignes de la procédure vue ci-dessus et la
troisième fait dérouler toutes ces
lignes de 1 à 20 pour obtenir 20 chiffres.
L'instruction evalf(…) calcule la fraction pour simple vérification. Chaque
chiffre sera placé en Ch dont les paramètres d'entrée sont n le rang de
l'itération (r = p/q), la fraction en cours d'étude à ce rang (cad:
multipliée par 10n). L'instruction
irem donne le reste de la division, ici par 10 (équivalent à mod 10); iquo
calcule le quotient; numer prend le numérateur de la fraction en le
multipliant par 10n et denom prend son dénominateur. L'instruction
séquence (seq) permet de former la liste des 20 chiffres demandés, chacun
étant l'évaluation de la fonction Ch pour n de 1 à 20. |
||
|
|
||
|
Programme selon la procédure vue ci-dessus
|
Programme qui calcule le nombre décimal à partir d'une fraction et en
isole les chiffres de la période. |
|
|
Explications La
séquence est répétée de 1 à q – 1 =
12. La
fonction calculée est celle vue ci-dessus: le quotient de 10 fois p par q. Sauf que
p évolue! En effet cette instruction seq, avec sont troisième argument, précise
que le reste de la division sera déposé en 'p'. Ainsi le nouveau p est égal à
l'ancien reste. |
||
|
Exemple avec partie non répétitive en tête
|
k évolue de 1 à 15 et non de 1 à q-1 car cette dernière valeur est
bien trop grande. |
|
Voir Programmation – Index
Bilan et Calcul direct avec Maple
|
Les
deux procédures d'extraction des chiffres sont équivalentes. La première
autorise n'importe quel numérateur, alors que la seconde impose la valeur 1. Notez
que le logiciel Maple possède une instruction particulière qui extrait la
période: pdexpand. |
|
|
|
L'instruction evalf effectue le développement décimal de 1/n L'instruction numtheory[expand] en donne les composantes: - le signe, - la partie entière, - la partie fixe décimale, et - les chiffres de la période. Pour isoler la période, on sélectionne le quatrième élément et on se
débarrasse du texte avec l'instruction op. |
Voir Application à l'extraction
de la période des nombres uniques
Extraction directe avec Maple
|
Maple dispose d'un jeu d'instructions
qui permet de travailler sur les nombres périodiques. Cherchez l'aide sur RepeatingDecimal. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Livres |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Nombre/aaaCycli/NbCycTH.htm
|
![]()