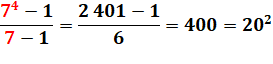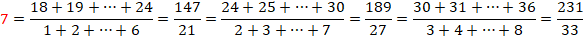nombre sept - maths

Nombre 7	Culture 7	Maths 7	7, …	Expressions en 7
Débutant 7	Culture suite 7	Divisibilité par 7	Table du 7	Proverbes avec 7
Quizz 7	Sciences 7	Division 1/7		Sept et Days
Horloge maths

Le chiffre sept avec ou sans barre

Quatre sept symétriques

Voir Barre du sept

Sept

Seven

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	111
Bases	11₆
Romain	VII

Suite

Plus petit nombre dont la somme des diviseurs est un cube. Suivants: 102, 110, 142, 159, 187, 381, 690, 714, 770, 994, 1034, …

Voir Partitions

Caractérisation du nombre

Singularité parmi les chiffres: tous peuvent être divisés ou multipliés sans quitter l'ensemble des chiffres. Seuls 5 et 7 résistent.

Le nombre 7 est le seul non atteignable par multiplication ou division avec les nombres de 1 à 10.

Auto-nombre

Brésilien (le plus petit)

Carol (2² – 1)² – 2

Chanceux d'Ulam

Congruent

Cunningham (2³ – 1)

Cyclique

Déficient

Dichotomique et trichotomique premier

Euclide premier

Factorielle première (3! + 1)

Fortuné

Glissant

Heegner

Heureux

Hofstadter – NON (le plus petit)

Hogben (3^e)

Idonéal

Impair

Kynea (2¹ + 1)² – 2

Lucas

Lucas premier (rang)

Mersenne (2³ – 1)

NSW (7² + 1 = 2 x 5²)

Padovan

Partition

Perrin (7^e)

Premier (le plus grand à un chiffre)

Premier cousin (2 fois: avec 3 et avec 11)

Premier cubain (2³ – 1³)

Premier de Bertrand

Premier de Carol et de Kynea

Premier de Chen

Premier de Mersenne (2³ – 1), le deuxième

Premier de Woodall (2 x 2² - 1)

Premier factoriel (3! + 1)

Premier fort

Premier horloge

Premier inévitable (ou minimal)

Premier jumeau avec 5

Premier long (1/7 = 0,142857 14…)

Premier minimal

Premier primorielle (5 =3# + 1)

Premier régulier

Premier sexy (avec 13)

Premier supersingulier

Premier sûr (2 x 3 + 1), le seul Mersenne et sûr

Somme diviseurs cube

Stirling 2^e espèce

Sylvester (1×2×3 + 1)

Tribonacci

Woodall (2×2² – 1), le plus petit premier

Zuckerman

Géométrique

Heptagonal (7^e)

Hexagonal centré (2^e)

2-pentagonal (2^e)

Octaédrique centré

Nombre tarte ou pizza (7 parts avec 3 découpes)

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Rappel Propriétés générales >>>

The doctor then told me that I should not do any events for three days and also said to me that I should not speak for three days. My wife said, 'make it seven'.

Alors mon docteur me dit que je devrais ni exercer une activité ni parler pendant trois jours. Ma femme dit: mettez sept jours

Arnold Schwartzeneger, Gouverneur de Californie après un accident de moto qui lui a valu une suture des lèvres.

Voir Pensées & humour / Expressions en anglais

PROPRIÉTÉS TYPIQUES

Nombre	7 = une pléiade Eu égard à son étymologie, certains souhaiteraient que une pléiade désigne sept choses. En fait, une pléiade désigne une multitude de choses.	>>>
	7 = 1 x 7 7 est un nombre premier. (3, 5, 7) seul triplet de nombres premiers impairs consécutifs	>>> >>>
	7 = 2³ – 1 Nombre de Mersenne premier (2^e). 2⁷ – 1 = 127 Nombre de Mersenne premier (4^e).	>>>
Numération	7₁₀ = 111₂ Nombre brésilien le plus petit.	>>>
	7 barres pour coder un chiffre sur un indicateur numérique.	>>>
Ésotérisme	7 est le plus populaire des nombres.	>>>
Arithmétique	7 = 1² + 1² + 1² + 2² Premier nombre somme de quatre carrés	>>>
	7⁰ + 7¹ + 7² + 7³ = 20² Seul cas de cette forme: somme des diviseurs du cube = carré.	>>>
	Seul chiffre (de 1 à 9) qui ne soit ni un multiple, ni un diviseur d'un nombre de 1 à 10 (2 divise 4, 3 divise 6..., 6 est un multiple de 2...)	>>>
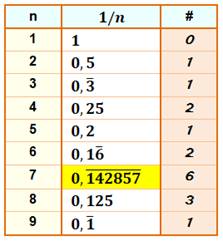
	999 999 / 7 = 142 857 Toutes les fractions avec 7 au dénominateur donnent ces chiffres avec permutation circulaire.	>>>
Dénombrer	7 est la quantité de manières de partitionner un ensemble de cinq objets identiques	>>>
Théorie des nombres	7 = 4 + 3 = 4² – 3² Motif valable pour tout nombre impair.	>>>
	Indétermination: sept cas dont le paradoxal 1^infini qui vaut 1 et bien d'autres valeurs.	>>>
	Les sept problèmes de la fondation Clay	>>>

Géométrie	7 triangles aigus minimum pour diviser un triangle obtus. Pour certains triangles, huit sont nécessaires.	>>>
	7 omniprésent dans les triplets de Pythagore.	>>>
	7 triangles de même aire divisent toujours un triangle quelconque.	>>>
	La dissection du carré en triangles semblables exige un minimum de sept d'entre eux.	>>>
	7 côtés: l'heptagone est le plus petit polygone qui ne peut pas être construit à la règle et au compas. Le suivant est l'ennéagone.	>>>
	7 régions créées par les côtés prolongés du triangle.	>>>
	7 tétrahexaminos Voir 16 tétra-bâtons	>>>
	Un ensemble de sept points mutuellement distance de 1 au moins est contenu dans un disque (y compris la frontière) de rayon 1 au moins.	>>>
	H = 7 Nombre de Heesch le plus petit sans solution connue. Notion de pavage fini.	>>>
Topologie	Les sept ponts de Königsberg résolu par Euler (1736).	>>>
	7 couleurs pour colorier le tore.	>>>
	Sphère à 7 dimensions => existence de plusieurs structures lisses: découverte de John Milnor 1963. Sphère à n dimensions => la généralisation existe effectivement => Topologie différentielle.	>>>
	Il existe 7 types de modèles de " catastrophes " en mathématiques.	>>>
Histoire	7 – Erdös: Nombre d'Erdös maximum.	>>>

SUITE >>>

PROPRIÉTÉS détaillées

Numération

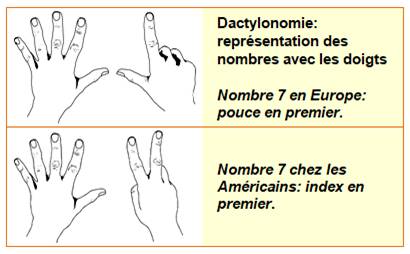
Voir Dactylonomie

7 = 111₂		Plus petit nombre brésilien: repdigit selon certaines bases de numération. Ici en binaire.
1 = 3 – 2 3 = 5 – 2 5 = 7 – 2	7 = / 9 = 11 – 2 11 = 13 – 2		Plus petit nombre impair non différence de deux nombres premiers.
7 = 6 + 1 = 2 x 2² – 1 = 1 x 8¹ – 1			Premier. Le plus petit de la forme 6n + 1. Premier de Woodall d'ordre 2 et d'ordre 8.
			Les nombres 3, 7 et 127 forment une unique chaine triple de nombres de Mersenne (premiers).
3 & 2 x 3 + 1 = 7 sont premiers			Premier sûr.
			Le nombre premier 7, de rang 4, est éloigné de 4 de deux autres nombres premiers.
7 = 3 + 4			Nombre de Lucas : 1, 3, 4, 7, 11, 18, 29...
1, 1, 2, 4, 7, 13, 24, 44, 81, 149 …			Nombre tribonacci. Sommes successives des trois nombres précédents.
17, 257, 65 537 …			Tous les nombres de Fermat se terminent par 7, à partir de F₂.
7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1			Cycle de Syracuse. Record d'altitude (3^e).
7 = 6 x 1 + 1			Nombre hexagonal centré.
7 = 2 x 3 + 1			Primorielle plus un, nombre premier.
7 = ½ 24/5 x 35/12 (25/5)² + (35/12)² = (337/60)²			7 est un nombre congruent. Triangle rectangle rationnel à aire rationnelle.
xy + x + y ne donne jamais 7			Auto-nombre.
7 mod 3 = 1 et mod 5 = 2			Nombre 2-chinois. Le plus petit. Suivant: 22.
7 = 3! + 1 7! – 1 = 5 039			Nombre premier factoriel. Générateur de nombre premier factoriel.
7 = 3! + 1 7! + 1 = 71²			Factorielle plus 1. Voir problème de Brocard en 4
7 = 3! + 1			3^e factorielle première; suivante: 11! + 1. Voir aussi Plage factorielle
– 7			Nombre de Heegner.
7, 16, 6, 52 Cycle: 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1			Le cycle de Syracuse de 7 comporte 16 étapes, un record. Il atteint une altitude maximale avec 52 au rang 6.

Addition

Diagramme de Ferrers du nombre 7

Voir Diagramme de Ferrers

7 = 1 + 2 + 4		Partition unique avec trois chiffres différents.
7 = 3 + 4 et 3 x 4 = 12		La bipartition qui donne el plus grand produit.
7 = P(5) partitions		Partitions du nombre 5.
		Somme de six nombres telle que mis sur un cercle, chacun est le produit des deux voisins.
7 = 1/4 x (1+2+3+4+5+6+7)		Le quart de la somme des nombres jusqu'à lui compris. >>>
7 + 7 + 7 = 21 = (1 + 2 + 3 + 4 + 5 + 6) / 3 = ((1+6) + (2+5) + (3+4)) /3		Le tiers des nombres qui lui sont inférieurs. Propriétés générale des impairs, liée à la formule donnant somme des entiers successifs S = n (n+1) /2.
7 P – P	Seul nombre impair non différence de deux premiers.

Multiplication

Table de multiplication du 7

Voir Table complète

Deux cas réputés difficiles; comment les mémoriser?

56 = 7 x 8 On note la suite des quatre chiffres: 5, 6, 7 et 8.

49 = 7 x 7 On se souvient que le carré est le nombre qui suit le produit des deux nombres voisins: 6 x 8 = 48 => 7 x 7 = 48 + 1 = 49.

Un schéma simple permet de se représenter les unités des multiplications par 7.

Pensez au clavier de votre ordinateur ou de votre calculette.

Partez du 7 et parcourez les chiffres de haut en bas et de gauche à droite, vous balayez les unités des multiplications par 7.

En effet: 7 x 1 = 7 et le suivant est bien 7x 2 = 14 se terminant par 4.

Arrivé en bas avec le 1, on constate que 7 x 3 est bien 21 avec un 1 pour unité. Etc.

Voir Tables de multiplication / Brève 441

1234 x 7 = 8 638 5050 2468 1120 8638		Multiplication rapide par 7: Mettre 5 sous tous les chiffres impairs, et Ajouter le double du chiffre du dessus, puis Ajouter la moitié entière du chiffre précédent.
x 7		Repdigit en 9 qui produit des repdigits partiels en 9 avec une multiplication par 7. Autres cas de production de repdigits partiels avec une multiplication par k >>>
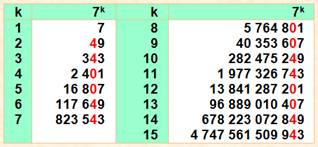
7 k	Pour les multiples de 7, les dizaines diminuées de deux fois les unités produisent un multiple de 7.
7 = 37 – 30	Nombre fortuné: différence entre primorielle et le premier juste plus grand (d'au moins 2).
7 multiplications	Nécessaire pour réaliser le produit de deux matrices 2×2. La solution classique exige huit multiplications. Une astuce permet d'accélérer cette opération.

Division

Division rapide par 7

Du fait que 13 x 7 = 91, on peut se ramener à une division par 91 en multipliant tout par 13.

Notez que:
91 x 11 = 1001

Application

Décimales de la période de 1/7 en un clin d'œil.

Voir Brève 568 / Divisibilité par 91 – Explications

	Nombre glissant.
7 = n.m / (n + m)	Pour deux couples de nombres seulement.
7 (2³ⁿ – 1)	Propriété générale des nombres de Mersenne composés. (Barre verticale = divise)
	Division avec des factorielles.
7 = 10! / 6!² = 10! / 720² = 3 628 800 / 518 400	Factorielle divisée. Seuls les chiffres 5, 6, 7 sont atteignables par cette forme. Le nombre suivant est 20.
		Motif général (exemple).
Div(64) = {1, 2, 4, 8, 16, 32, 64}	Plus petit nombre possédant sept diviseurs.
89, 90, 91, 92, 93, 94, 95, 96, 97	Plus petit cas pour sept nombres composés de suite.
	La somme des diviseurs est un cube.
	Un seul antécédent aliquote, le nombre 8.
	Plus petit cas pour sept égalités de phi, la quantité de nombres premiers inférieurs à n.

Divisibilité

Clé de divisibilité par 7.

Soustraite deux fois les unités aux dizaines.

Le résultat doit être divisible par 7.

Si le nombre est grand, refaire l'opération.

Ex: 8 638 => 863 – 16 = 847; 84 – 14 = 70

Divisibilité par 7

Tous les procédés ont un point commun: leurs calculs sont plus longs que la division par 7.

6ⁿ – 5ⁿ + 4ⁿ – 3ⁿ + 2ⁿ – 1ⁿ

Divisible par 7 pour les puissances paires.

abc abc

est divisible par 7

Exemples:

123123 = 3 x 17 589

454454 = 3 x 64 922

n⁶ – 1

est divisible par 7

si n non divisible par 7

Exemples:

2⁶ – 1 = 63

3⁶ – 1 = 728 = 7 x 104

4⁶ – 1 = 4 095 = 7 x 586

4ⁿ – 3ⁿ

est divisible par 7

pour n pair

Exemples:

4² – 3² = 7

4⁴ – 3⁴ = 175 = 7 x 25

3²ⁿ – 2ⁿ

est divisible par 7

Exemples:

3² - 2 = 7

3⁴ - 2² = 77

3⁶ - 2³ = 721 = 7 x 103

7 p¹² – q¹²

Divisibilité par 7

si p ou q non divisibles par 7.

Divisibilité par 7. Démonstration.

Fraction 1 / 7

	Plus petit nombre dont l'inverse s'écrit avec plus de deux chiffres. Le surlignement indique que ce nombre est répété indéfiniment. Voir Nombres périodiques
142 + 857 = 999 14 + 28 + 57 = 99	Division par 7 et nombres périodiques: le nombre 7 est dichotomique et trichotomique premier; les demi-périodes de 1/7, comme ses tiers de période, somment en nombres en 9.
1/7= 0,142857 1428… 2/7 = 0,285714 2257… 142 857 x 7 = 999 999	Ce nombre est magique! Les nombres entiers divisés par 7 produisent les mêmes décimales périodiques d'ordre 6 par permutations circulaires.
	Nombre têtu. Seul nombre qui multiplié par 1, 2, 3, 4, 5 ou 6 donne un produit toujours formé des mêmes chiffres.

Voir Nombre 142 857 / Nombre 1/7 = 0, 142…

Constantes et approximations en septièmes

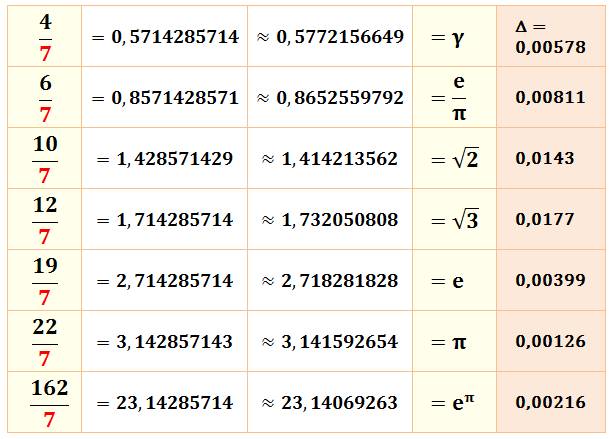
Puissances

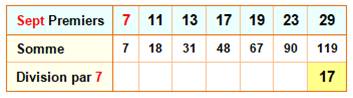
7 = 1² + 1² + 1² + 2²	Théorème de Waring Tout entier est décomposable en somme d'au plus 4 carrés. Le nombre 4 exige les 4 termes. Tout nombre suffisamment grand peut s'écrire comme la somme d'au plus sept cubes. Tout nombre est la somme d'au plus sept nombres premiers (Olivier Ramaré – 1995). Tout nombre impair est la somme d'au plus cinq nombres premiers (Terence Tao – 2012). Tout nombre impair est la somme d'au plus trois nombres premiers (Conjecture de Goldbach). Plus petit nombre à ne pas être somme de trois carrés. Voir décomposition Seule somme de puissances de 2 à 5 avec deux à cinq termes.
7 = 3² – 3 + 1	Nombre polygonal centré d'ordre 2 ou nombre de Hogben.
7 = 2⁰ + 2¹ + 2² = 2³ – 1	Somme puissances successives. Cette égalité est une propriété générale.
7 = 4 + 3 = 4² – 3²	Motif valable pour tout nombre impair.
= 2,370370… + 4,6296296…			Différence et somme de deux cubes rationnels.
7 = 4² – 3² 4³ – 3³ = 37	Nombre binomial. Différence de deux carrés consécutifs. Premier-"cubes".
7 = 2^{3 – 1} + 3	Nombre premier en puissance de 2. Rare. Liste: 1, 3, 7, 237, 1 885, 51 381…
7 = 2⁴ – 3² = 16 – 9 = 2⁵ – 5² = 32 – 25 = 2⁷ – 11² = 128 – 121 = 2¹⁵ – 181² = 32 768 – 32761 = 8⁵ – 181² = 32 768 – 32 761 = 32³ – 181² = 32 768 – 32 761		Différence de puissances successives.
7 = 2³ – 1 = 2³ – 1³		Nombre de Mersenne. Différence de deux cubes consécutifs (nombre cubain).
4² – 3² = 7 4⁴ – 3⁴ = 175 = 7 x 25 4ⁿ – 3ⁿ = 7 k		Motif divisible par 7 pour les puissances paires.
7 cubes		Tous les nombres (grands) sont sommes de 7 cubes.
7 = (–1)³ + (0)³ + 2³ = 32³ + 104³ + (–105)³ = 44³ + 68³ + (–169)³ = …		Partition du nombre 7 en sommes de cubes.
		Formule sur le modèle Bombelli.
		Nombre d'or et son inverse.

Puissances du nombre

Voir Puissance / Racine

7² = 2 x 5² – 1 49 = 2 x 25 – 1	Une des solutions de l'équation de Pell-Fermat: x² – 2y² + 1 = 0.
7² = 5² + 5² – 1	7 est presque la diagonale d'un carré de côté 5. Les Grecs l'appelaient la diagonale rationnelle.
7² = 2² + 3² + 6²	Carré somme de trois carrés, comme tous les carrés impairs. Le dernier en telle somme unique.
7² = 25² – 24² = 25 + 24	Triplet de Pythagore jumeau.
7³ = (3 + 4)³ = 343	Curiosité et truc pour mémoriser le cube de 7. Palindrome.
7³ = 18⁰ + 18¹ + 18² = 1 + 18 + 324 = 343 = 7³	Deux des trois cas de puissances successives comme puissance.
	Un des trois tels motifs.
7⁰ + 7¹ + 7² + 7³ = 1 + 7 + 49 + 343 = 400 = 20²	Curiosité. Seul entier tel que la somme des diviseurs de son cube (1, 7, 49 et 343) soit un carré.
7³ = 343 = 122 + 221 = 320 + 23	Cube palindrome et avec chiffres 3 et 4. Cube avec nombres ajoutés à leur retourné.
7⁴= 2 401 & 2 + 4 + 0 + 1 = 7	Bicarré avec chiffres jusqu'à 4. Nombre de Kaprekar d'ordre 4. Nombre NESCHIP.
7⁷ = 823 543 6 mod 11	Méthode de calcul avec Fermat.
7ⁿ 7² – 1 = 48 7⁴ – 1 = 2400 7⁶ – 1 = 117648 …	Toutes les puissances paires de 7, moins 1, sont divisibles par 48 Sinon (impair): divisible par 6.
7² = 49, 7³ = 343 … 7^k d = 0 ou 4 Exemple: 7³³ = … xy 33 = 4 x 8 + 1 => xy = 01	Le chiffre des dizaines de 7 à la puissance k est toujours 0 ou 4. Le chiffre des unités est 1, 7, 9, 3
7 = SCh(2⁴, 4², 4⁵, 5², 7⁴, 32², 49²) 16, 16, 1024, 25, 2401, 1024, 2401		Puissances dont la somme des chiffres vaut 7.

Autour du nombre

7 – 2¹ = 5 et 7 – 2² = 3		Sont tous deux premiers.
(7, 17, 23)		Triplet tel qu'en ajoutant 73 à chacun, le premier est égal double de la somme des deux autres, le deuxième est égal au triple et le troisième au quadruple. Voir Explications
7! + 1 = 5 041 = 71²		Problème de Brocard. 3^e et dernière solution.
		Nombre premier. Expression première pour: 3, 5, 7, 71, 151, 157 (testée jusqu'à 1000).
			Nombre d'Armstrong. Le plus petit.
			Curiosité. Citée par Daniel Lignon – Dictionnaire de (presque) tous les nombres entiers – Page 109
7 chiffres dans 1212121		Le plus petit nombre premier ondulant en 12. Le suivant a 11 chiffres
7, 37, 67, 97, 127, 157 107, 137, 167, 197, 227, 257		Six nombres premiers en 7 et en progression arithmétique de 30; et même, une seconde progression de six commençant par 107.
7, 907, 9 907, 99 907, 999 907 et 9 999 907		Sont premiers. Le dernier a sept chiffres.
568⁷ = 127⁷ + 258⁷ + 266⁷ + 413⁷ + 430⁷ + 469⁷ + 525⁷		Puissance septième somme de sept puissances septièmes (Mark Dodrill – 1999).
777	Nombre qui porte chance. Sur les machines à sous, il indique le jackpot. Nombre de la perfection (contesté). Voir Nombre 777

Jeux et curiosités

Question: Si 2x = 5y que dire de la somme x + y ?

Solution: formons cette somme à gauche:

2x + 2y = 5y + 2y = 2(x + y) = 7y

La somme est un multiple de 7.

7 = 1 + 6 = 2 + 5 = 3 + 4 = 7 3 x 7 = 21		Somme des faces opposées d'un dé. Somme totale des points sur un dé: facile à retenir, c'est trois double-faces à 7 points, c'est-à-dire la somme des nombres de 1 à 6, qui est le nombre triangulaire 21 .
		Divisions pannumériques avec quotient égal à 7. Il y en a sept.
7 x 9 304 = 65 128		Opération pannumérique (de 0 à 9).
7 x 1 359 = 9 513 7 x 11 688 = 81 816 7 x 11 883 = 83 181 …		Produits qui conservent les chiffres.
7 = (Ö9)! + 9/9 = 6 + 1		Faire 7 avec k chiffres identiques.
		Comment écrire 7 avec des puissances de 3.
	Jeu du quatre 4.
7 = 9 – 2 77 = 9² – 2² …	Motifs produisant une persistance du 7.
Ordre 7	Ordre du plus petit cube magique parfait multiplicatif connu (Christian Boyer – 2006)
		Mêmes chiffres de part et d'autre de l'égalité.
		Curiosité avec la racine quatrième.

Nombre 7 et ses décimales >>>

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]

Repdigit (Brésilien)

2, [1, 1, 1]

3, [2, 1]

4, [1, 3]

5, [1, 2]

6, [1, 1]

7, [1, 0]

2, [1, 1, 1]

6, [1, 1]

Voir Bases / Brésiliens

Suite	Voir le menu en haut de page Nombre 7 en sciences et divers Multiplication 77
Voir	Nombre Hexagonal Centré Triangle en 7
Site	Références Internet
Cette page	http://villemin.gerard.free.fr/NombDico/SeptP11.htm

Renvoi de lien

SOLITAIRE >>>